| << Chapter < Page | Chapter >> Page > |
Consider a uniform (density and shape) thin rod of mass M and length L as shown in [link] . We want a thin rod so that we can assume the cross-sectional area of the rod is small and the rod can be thought of as a string of masses along a one-dimensional straight line. In this example, the axis of rotation is perpendicular to the rod and passes through the midpoint for simplicity. Our task is to calculate the moment of inertia about this axis. We orient the axes so that the z -axis is the axis of rotation and the x -axis passes through the length of the rod, as shown in the figure. This is a convenient choice because we can then integrate along the x -axis.
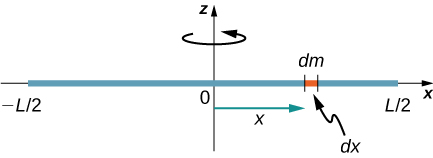
We define dm to be a small element of mass making up the rod. The moment of inertia integral is an integral over the mass distribution. However, we know how to integrate over space, not over mass. We therefore need to find a way to relate mass to spatial variables. We do this using the linear mass density of the object, which is the mass per unit length. Since the mass density of this object is uniform, we can write
If we take the differential of each side of this equation, we find
since is constant. We chose to orient the rod along the x -axis for convenience—this is where that choice becomes very helpful. Note that a piece of the rod dl lies completely along the x -axis and has a length dx ; in fact, in this situation. We can therefore write , giving us an integration variable that we know how to deal with. The distance of each piece of mass dm from the axis is given by the variable x , as shown in the figure. Putting this all together, we obtain
The last step is to be careful about our limits of integration. The rod extends from to , since the axis is in the middle of the rod at . This gives us
Next, we calculate the moment of inertia for the same uniform thin rod but with a different axis choice so we can compare the results. We would expect the moment of inertia to be smaller about an axis through the center of mass than the endpoint axis, just as it was for the barbell example at the start of this section. This happens because more mass is distributed farther from the axis of rotation.
Now consider the same uniform thin rod of mass M and length L , but this time we move the axis of rotation to the end of the rod. We wish to find the moment of inertia about this new axis ( [link] ). The quantity dm is again defined to be a small element of mass making up the rod. Just as before, we obtain
However, this time we have different limits of integration. The rod extends from to , since the axis is at the end of the rod at . Therefore we find

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?