| << Chapter < Page | Chapter >> Page > |
We select the pivot at point P (upper hinge, per the free-body diagram) and write the second equilibrium condition for torques in rotation about point P :
We use the free-body diagram to find all the terms in this equation:
In evaluating we use the geometry of the triangle shown in part (a) of the figure. Now we substitute these torques into [link] and compute
Therefore the magnitudes of the horizontal component forces are The forces on the door are
The forces on the hinges are found from Newton’s third law as
Check Your Understanding Solve the problem in [link] by taking the pivot position at the center of mass.
Check Your Understanding A 50-kg person stands 1.5 m away from one end of a uniform 6.0-m-long scaffold of mass 70.0 kg. Find the tensions in the two vertical ropes supporting the scaffold.
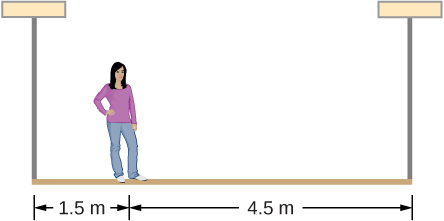
711.0 N; 466.0 N
Check Your Understanding A 400.0-N sign hangs from the end of a uniform strut. The strut is 4.0 m long and weighs 600.0 N. The strut is supported by a hinge at the wall and by a cable whose other end is tied to the wall at a point 3.0 m above the left end of the strut. Find the tension in the supporting cable and the force of the hinge on the strut.
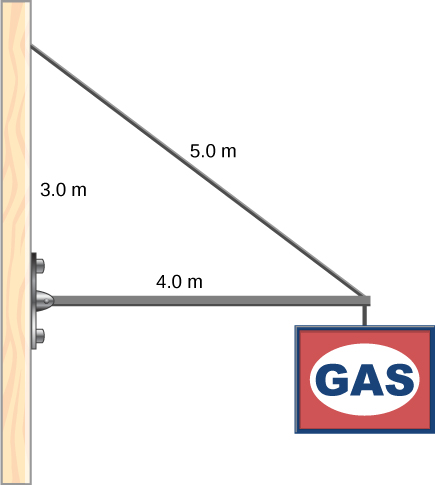
1167 N; 980 N directed upward at above the horizontal
Is it possible to rest a ladder against a rough wall when the floor is frictionless?
Show how a spring scale and a simple fulcrum can be used to weigh an object whose weight is larger than the maximum reading on the scale.
(Proof)

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?