| << Chapter < Page | Chapter >> Page > |
Why do roofs of gymnasiums and churches seem to fail more than family homes when an earthquake occurs?
Wine glasses can be set into resonance by moistening your finger and rubbing it around the rim of the glass. Why?
Energy is supplied to the glass by the work done by the force of your finger on the glass. When supplied at the right frequency, standing waves form. The glass resonates and the vibrations produce sound.
Air conditioning units are sometimes placed on the roof of homes in the city. Occasionally, the air conditioners cause an undesirable hum throughout the upper floors of the homes. Why does this happen? What can be done to reduce the hum?
Consider a standing wave modeled as Is there a node or an antinode at What about a standing wave modeled as Is there a node or an antinode at the position?
For the equation there is a node because when , so for all time. For the equation there is an antinode because when , , so oscillates between + A and − A as the cosine term oscillates between +1 and -1.
A wave traveling on a Slinky® that is stretched to 4 m takes 2.4 s to travel the length of the Slinky and back again. (a) What is the speed of the wave? (b) Using the same Slinky stretched to the same length, a standing wave is created which consists of three antinodes and four nodes. At what frequency must the Slinky be oscillating?
A 2-m long string is stretched between two supports with a tension that produces a wave speed equal to What are the wavelength and frequency of the first three modes that resonate on the string?
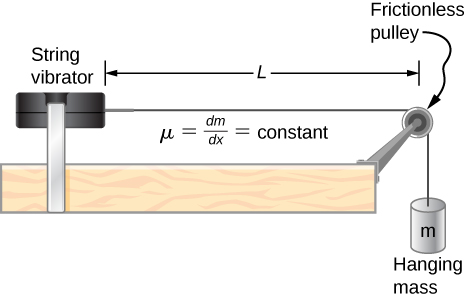
Consider the experimental setup shown below. The length of the string between the string vibrator and the pulley is The linear density of the string is The string vibrator can oscillate at any frequency. The hanging mass is 2.00 kg. (a)What are the wavelength and frequency of mode? (b) The string oscillates the air around the string. What is the wavelength of the sound if the speed of the sound is
A cable with a linear density of is hung from telephone poles. The tension in the cable is 500.00 N. The distance between poles is 20 meters. The wind blows across the line, causing the cable resonate. A standing waves pattern is produced that has 4.5 wavelengths between the two poles. The air temperature is What are the frequency and wavelength of the hum?
Consider a rod of length L , mounted in the center to a support. A node must exist where the rod is mounted on a support, as shown below. Draw the first two normal modes of the rod as it is driven into resonance. Label the wavelength and the frequency required to drive the rod into resonance.
Consider two wave functions and . Write a wave function for the resulting standing wave.

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?