| << Chapter < Page | Chapter >> Page > |
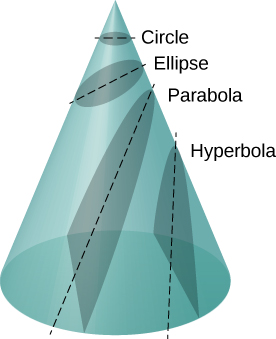
If the total energy is negative, then , and [link] represents a bound or closed orbit of either an ellipse or a circle, where . [You can see from [link] that for , , and hence the radius is constant.] For ellipses, the eccentricity is related to how oblong the ellipse appears. A circle has zero eccentricity, whereas a very long, drawn-out ellipse has an eccentricity near one.
If the total energy is exactly zero, then and the path is a parabola. Recall that a satellite with zero total energy has exactly the escape velocity. (The parabola is formed only by slicing the cone parallel to the tangent line along the surface.) Finally, if the total energy is positive, then and the path is a hyperbola. These last two paths represent unbounded orbits, where m passes by M once and only once. This situation has been observed for several comets that approach the Sun and then travel away, never to return.
We have confined ourselves to the case in which the smaller mass (planet) orbits a much larger, and hence stationary, mass (Sun), but [link] also applies to any two gravitationally interacting masses. Each mass traces out the exact same-shaped conic section as the other. That shape is determined by the total energy and angular momentum of the system, with the center of mass of the system located at the focus. The ratio of the dimensions of the two paths is the inverse of the ratio of their masses.
You can see an animation of two interacting objects at the My Solar System page at Phet . Choose the Sun and Planet preset option. You can also view the more complicated multiple body problems as well. You may find the actual path of the Moon quite surprising, yet is obeying Newton’s simple laws of motion.
People have imagined traveling to the other planets of our solar system since they were discovered. But how can we best do this? The most efficient method was discovered in 1925 by Walter Hohmann, inspired by a popular science fiction novel of that time. The method is now called a Hohmann transfer . For the case of traveling between two circular orbits, the transfer is along a “transfer” ellipse that perfectly intercepts those orbits at the aphelion and perihelion of the ellipse. [link] shows the case for a trip from Earth’s orbit to that of Mars. As before, the Sun is at the focus of the ellipse.
For any ellipse, the semi-major axis is defined as one-half the sum of the perihelion and the aphelion. In [link] , the semi-major axis is the distance from the origin to either side of the ellipse along the x -axis, or just one-half the longest axis (called the major axis). Hence, to travel from one circular orbit of radius to another circular orbit of radius , the aphelion of the transfer ellipse will be equal to the value of the larger orbit, while the perihelion will be the smaller orbit. The semi-major axis, denoted a , is therefore given by .

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?