-
Home
- University physics volume 1
- Unit 1. mechanics
- Linear momentum and collisions
- Rocket propulsion
Two billiard balls are at rest and touching each other on a pool table. The cue ball travels at 3.8 m/s along the line of symmetry between these balls and strikes them simultaneously. If the collision is elastic, what is the velocity of the three balls after the collision?
final velocity of cue ball is
, final velocities of the other two balls are 2.6 m/s at ±30° with respect to the initial velocity of the cue ball
Got questions? Get instant answers now!
A billiard ball traveling at
collides with a wall that is aligned in the
direction. Assuming the collision is elastic, what is the final velocity of the ball?
Got questions? Get instant answers now!
Two identical billiard balls collide. The first one is initially traveling at
and the second one at
. Suppose they collide when the center of ball 1 is at the origin and the center of ball 2 is at the point
where
R is the radius of the balls. What is the final velocity of each ball?
ball 1:
, ball 2:
Got questions? Get instant answers now!
Repeat the preceding problem if the balls collide when the center of ball 1 is at the origin and the center of ball 2 is at the point
ball 1:
, ball 2:
Got questions? Get instant answers now!
Where is the center of mass of a slice of pizza that was cut into eight equal slices? Assume the origin is at the apex of the slice and measure angles with respect to an edge of the slice. The radius of the pizza is
R .
Got questions? Get instant answers now!
If the entire population of Earth were transferred to the Moon, how far would the center of mass of the Earth-Moon-population system move? Assume the population is 7 billion, the average human has a mass of 65 kg, and that the population is evenly distributed over both the Earth and the Moon. The mass of the Earth is
and that of the Moon is
. The radius of the Moon’s orbit is about
.
Got questions? Get instant answers now!
You friend wonders how a rocket continues to climb into the sky once it is sufficiently high above the surface of Earth so that its expelled gasses no longer push on the surface. How do you respond?
Answers may vary. The rocket is propelled forward not by the gasses pushing against the surface of Earth, but by conservation of momentum. The momentum of the gas being expelled out the back of the rocket must be compensated by an increase in the forward momentum of the rocket.
Got questions? Get instant answers now!
Challenge
A 65-kg person jumps from the first floor window of a burning building and lands almost vertically on the ground with a horizontal velocity of 3 m/s and vertical velocity of
. Upon impact with the ground he is brought to rest in a short time. The force experienced by his feet depends on whether he keeps his knees stiff or bends them. Find the force on his feet in each case.

- First find the impulse on the person from the impact on the ground. Calculate both its magnitude and direction.
- Find the average force on the feet if the person keeps his leg stiff and straight and his center of mass drops by only 1 cm vertically and 1 cm horizontally during the impact.
- Find the average force on the feet if the person bends his legs throughout the impact so that his center of mass drops by 50 cm vertically and 5 cm horizontally during the impact.
- Compare the results of part (b) and (c), and draw conclusions about which way is better.
You will need to find the time the impact lasts by making reasonable assumptions about the deceleration. Although the force is not constant during the impact, working with constant average force for this problem is acceptable.
a.
, 108°; b.
,
; c.
,
Got questions? Get instant answers now!
Two projectiles of mass
and
are fired at the same speed but in opposite directions from two launch sites separated by a distance
D . They both reach the same spot in their highest point and strike there. As a result of the impact they stick together and move as a single body afterwards. Find the place they will land.
Got questions? Get instant answers now!
Two identical objects (such as billiard balls) have a one-dimensional collision in which one is initially motionless. After the collision, the moving object is stationary and the other moves with the same speed as the other originally had. Show that both momentum and kinetic energy are conserved.
Conservation of momentum demands
. We are given that
,
, and
. Combining these equations with the equation given by conservation of momentum gives
, which is true, so conservation of momentum is satisfied. Conservation of energy demands
. Again combining this equation with the conditions given above give
, so conservation of energy is satisfied.
Got questions? Get instant answers now!
A ramp of mass
M is at rest on a horizontal surface. A small cart of mass
m is placed at the top of the ramp and released.
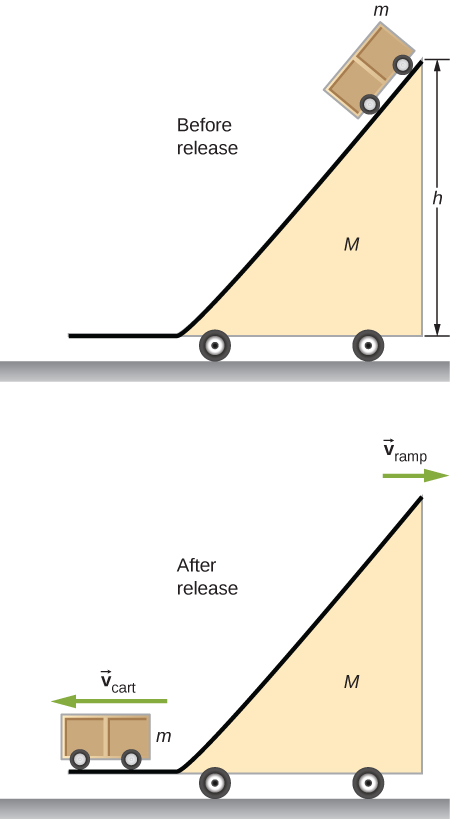
What are the velocities of the ramp and the cart relative to the ground at the instant the cart leaves the ramp?
Got questions? Get instant answers now!
Find the center of mass of the structure given in the figure below. Assume a uniform thickness of 20 cm, and a uniform density of
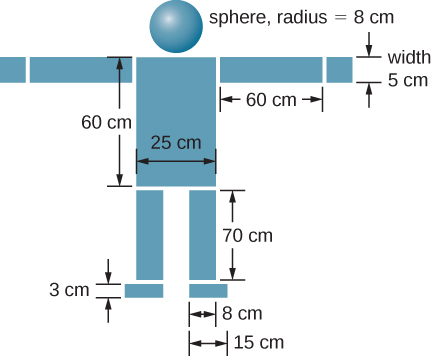
Assume origin on centerline and at floor, then
Got questions? Get instant answers now!
Questions & Answers
Three charges q_{1}=+3\mu C, q_{2}=+6\mu C and q_{3}=+8\mu C are located at (2,0)m (0,0)m and (0,3) coordinates respectively. Find the magnitude and direction acted upon q_{2} by the two other charges.Draw the correct graphical illustration of the problem above showing the direction of all forces.
To solve this problem, we need to first find the net force acting on charge q_{2}. The magnitude of the force exerted by q_{1} on q_{2} is given by F=\frac{kq_{1}q_{2}}{r^{2}} where k is the Coulomb constant, q_{1} and q_{2} are the charges of the particles, and r is the distance between them.
Muhammed
What is the direction and net electric force on q_{1}= 5µC located at (0,4)r due to charges q_{2}=7mu located at (0,0)m and q_{3}=3\mu C located at (4,0)m?
what is the change in momentum of a body?
Capacitor is a separation of opposite charges using an insulator of very small dimension between them. Capacitor is used for allowing an AC (alternating current) to pass while a DC (direct current) is blocked.
Gautam
A motor travelling at 72km/m on sighting a stop sign applying the breaks such that under constant deaccelerate in the meters of 50 metres what is the magnitude of the accelerate
What is Thermodynamics
Muordit
velocity can be 72 km/h in question. 72 km/h=20 m/s, v^2=2.a.x , 20^2=2.a.50, a=4 m/s^2.
Mehmet
A boat travels due east at a speed of 40meter per seconds across a river flowing due south at 30meter per seconds. what is the resultant speed of the boat
50 m/s due south east
Someone
which has a higher temperature, 1cup of boiling water or 1teapot of boiling water which can transfer more heat 1cup of boiling water or 1 teapot of boiling water explain your . answer
I believe temperature being an intensive property does not change for any amount of boiling water whereas heat being an extensive property changes with amount/size of the system.
Someone
temperature for any amount of water to boil at ntp is 100⁰C (it is a state function and and intensive property) and it depends both will give same amount of heat because the surface available for heat transfer is greater in case of the kettle as well as the heat stored in it but if you talk.....
Someone
about the amount of heat stored in the system then in that case since the mass of water in the kettle is greater so more energy is required to raise the temperature b/c more molecules of water are present in the kettle
Someone
physics, biology and chemistry
this is my Field
ALIYU
field is a region of space under the influence of some physical properties
Collete
what is ogarnic chemistry
determine the slope giving that 3y+ 2x-14=0
WISDOM
Another formula for Acceleration
pratica A on solution of hydro chloric acid,B is a solution containing 0.5000 mole ofsodium chlorid per dm³,put A in the burret and titrate 20.00 or 25.00cm³ portion of B using melting orange as the indicator. record the deside of your burret tabulate the burret reading and calculate the average volume of acid used?
how do lnternal energy measures
Esrael
Two bodies attract each other electrically. Do they both have to be charged? Answer the same question if the bodies repel one another.
No. According to Isac Newtons law. this two bodies maybe you and the wall beside you.
Attracting depends on the mass och each body and distance between them.
Dlovan
Are you really asking if two bodies have to be charged to be influenced by Coulombs Law?
Robert
like charges repel while unlike charges atttact
Raymond
What is specific heat capacity
Specific heat capacity is a measure of the amount of energy required to raise the temperature of a substance by one degree Celsius (or Kelvin). It is measured in Joules per kilogram per degree Celsius (J/kg°C).
AI-Robot
specific heat capacity is the amount of energy needed to raise the temperature of a substance by one degree Celsius or kelvin
ROKEEB
Got questions? Join the online conversation and get instant answers!
Source:
OpenStax, University physics volume 1. OpenStax CNX. Sep 19, 2016 Download for free at http://cnx.org/content/col12031/1.5
Google Play and the Google Play logo are trademarks of Google Inc.



