| << Chapter < Page | Chapter >> Page > |
As we saw in Applications of Newton’s Laws , objects moving at constant speed in a circle have a centripetal acceleration directed toward the center of the circle, which means that there must be a net force directed toward the center of that circle. Since all objects on the surface of Earth move through a circle every 24 hours, there must be a net centripetal force on each object directed toward the center of that circle.
Let’s first consider an object of mass m located at the equator, suspended from a scale ( [link] ). The scale exerts an upward force away from Earth’s center. This is the reading on the scale, and hence it is the apparent weight of the object. The weight ( mg ) points toward Earth’s center. If Earth were not rotating, the acceleration would be zero and, consequently, the net force would be zero, resulting in . This would be the true reading of the weight.
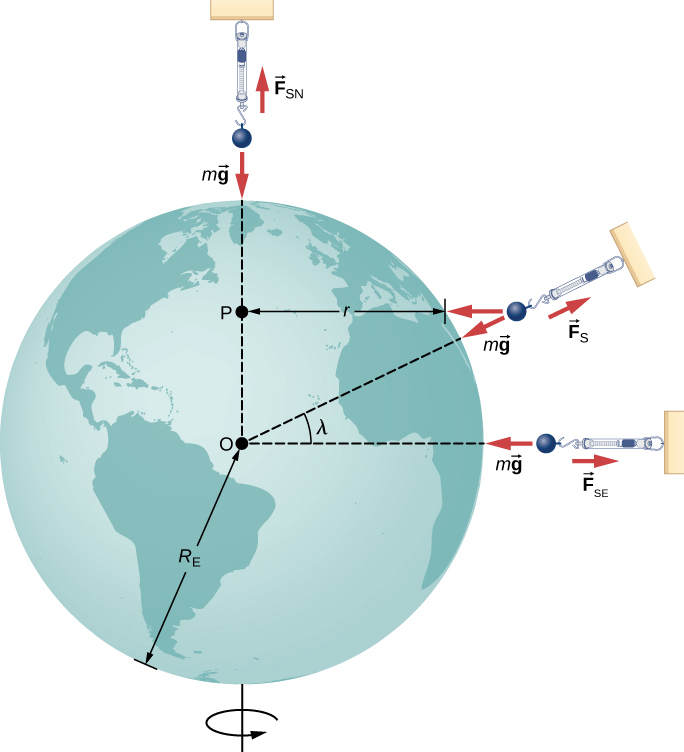
With rotation, the sum of these forces must provide the centripetal acceleration, . Using Newton’s second law, we have
Note that points in the same direction as the weight; hence, it is negative. The tangential speed v is the speed at the equator and r is . We can calculate the speed simply by noting that objects on the equator travel the circumference of Earth in 24 hours. Instead, let’s use the alternative expression for from Motion in Two and Three Dimensions . Recall that the tangential speed is related to the angular speed by . Hence, we have . By rearranging [link] and substituting , the apparent weight at the equator is
The angular speed of Earth everywhere is
Substituting for the values or and , we have . This is only 0.34% of the value of gravity, so it is clearly a small correction.
The period T is the time for one complete rotation. Therefore, the tangential speed is the circumference divided by T , so we have
This is about 84 minutes.

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?