| << Chapter < Page | Chapter >> Page > |
Whenever we have two-dimensional vector problems in which no two vectors are parallel, the easiest method of solution is to pick a convenient coordinate system and project the vectors onto its axes. In this case, the best coordinate system has one horizontal axis ( x ) and one vertical axis ( y ).
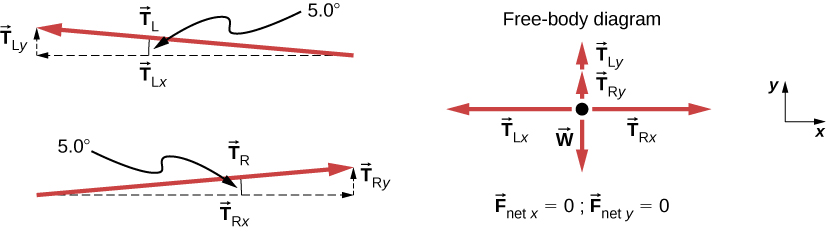
Consider the horizontal components of the forces (denoted with a subscript x ):
The net external horizontal force since the person is stationary. Thus,
Now observe [link] . You can use trigonometry to determine the magnitude of and :
Equating T L x and T R x :
Thus,
as predicted. Now, considering the vertical components (denoted by a subscript y ), we can solve for T . Again, since the person is stationary, Newton’s second law implies that . Thus, as illustrated in the free-body diagram,
We can use trigonometry to determine the relationships among and T . As we determined from the analysis in the horizontal direction, :
Now we can substitute the vales for and , into the net force equation in the vertical direction:
and
so
and the tension is
If we wish to create a large tension, all we have to do is exert a force perpendicular to a taut flexible connector, as illustrated in [link] . As we saw in [link] , the weight of the tightrope walker acts as a force perpendicular to the rope. We saw that the tension in the rope is related to the weight of the tightrope walker in the following way:
We can extend this expression to describe the tension T created when a perpendicular force is exerted at the middle of a flexible connector:
The angle between the horizontal and the bent connector is represented by . In this case, T becomes large as approaches zero. Even the relatively small weight of any flexible connector will cause it to sag, since an infinite tension would result if it were horizontal (i.e., and sin ). For example, [link] shows a situation where we wish to pull a car out of the mud when no tow truck is available. Each time the car moves forward, the chain is tightened to keep it as straight as possible. The tension in the chain is given by and since is small, T is large. This situation is analogous to the tightrope walker, except that the tensions shown here are those transmitted to the car and the tree rather than those acting at the point where is applied.

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?