1. Home
  2. University physics volume 1
  3. Unit 1. mechanics
  4. Motion in two and three dimensions
  5. Acceleration vector

4.2 Acceleration vector  (Page 2/4)

<< Chapter < Page
  University physics volume 1     Page 2 / 4
Chapter >> Page >
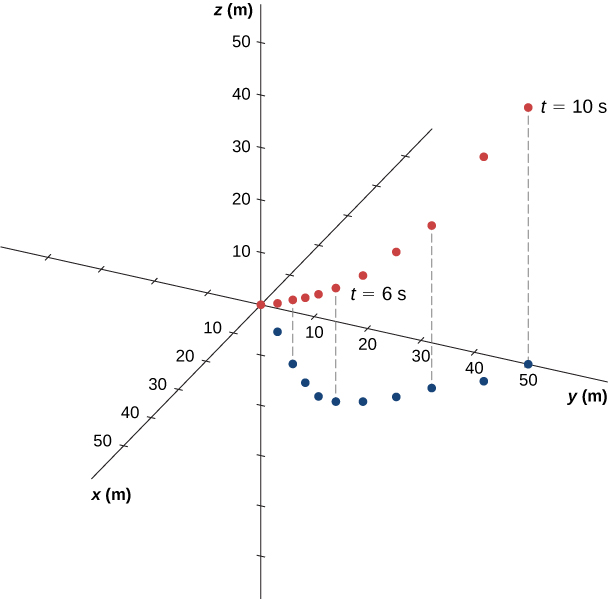
An x y z coordinate system is shown. All the axes show distance in meters and run from -50 to 50 meters. A series of 10 red dots are shown, with the sixth dot is labeled as t = 6 s and the tenth as t = 10 s. The red series of dots starts at the origin and curves upward (both y and z increasing with time). Vertical dashed lines connect the red dots to a series of blue dots in the x y plane. The blue dots are all in the first quadrant (positive x and y). The dots are regularly spaced along the y coordinate, while the x coordinate starts at 0, increases, reaches a maximum of x = 25 m at t = 5, and then decreases back to x = 0 at t 10 s.
The particle starts at point ( x , y , z ) = (0, 0, 0) with position vector r → = 0 . The projection of the trajectory onto the xy- plane is shown. The values of y and z increase linearly as a function of time, whereas x has a turning point at t = 5 s and 25 m, when it reverses direction. At this point, the x component of the velocity becomes negative. At t = 10 s, the particle is back to 0 m in the x direction.

Significance

By graphing the trajectory of the particle, we can better understand its motion, given by the numerical results of the kinematic equations.

Check Your Understanding Suppose the acceleration function has the form a → ( t ) = a i ^ + b j ^ + c k ^ m/ s 2 , where a, b, and c are constants. What can be said about the functional form of the velocity function?

The acceleration vector is constant and doesn’t change with time. If a, b , and c are not zero, then the velocity function must be linear in time. We have v → ( t ) = ∫ a → d t = ∫ ( a i ^ + b j ^ + c k ^ ) d t = ( a i ^ + b j ^ + c k ^ ) t m/s , since taking the derivative of the velocity function produces a → ( t ) . If any of the components of the acceleration are zero, then that component of the velocity would be a constant.

Got questions? Get instant answers now!

Constant acceleration

Multidimensional motion with constant acceleration can be treated the same way as shown in the previous chapter for one-dimensional motion. Earlier we showed that three-dimensional motion is equivalent to three one-dimensional motions, each along an axis perpendicular to the others. To develop the relevant equations in each direction, let’s consider the two-dimensional problem of a particle moving in the xy plane with constant acceleration, ignoring the z -component for the moment. The acceleration vector is

a → = a 0 x i ^ + a 0 y j ^ .

Each component of the motion has a separate set of equations similar to [link] – [link] of the previous chapter on one-dimensional motion. We show only the equations for position and velocity in the x - and y -directions. A similar set of kinematic equations could be written for motion in the z -direction:

x ( t ) = x 0 + ( v x ) avg t
v x ( t ) = v 0 x + a x t
x ( t ) = x 0 + v 0 x t + 1 2 a x t 2
v x 2 ( t ) = v 0 x 2 + 2 a x ( x − x 0 )
y ( t ) = y 0 + ( v y ) avg t
v y ( t ) = v 0 y + a y t
y ( t ) = y 0 + v 0 y t + 1 2 a y t 2
v y 2 ( t ) = v 0 y 2 + 2 a y ( y − y 0 ) .

Here the subscript 0 denotes the initial position or velocity. [link] to [link] can be substituted into [link] and [link] without the z -component to obtain the position vector and velocity vector as a function of time in two dimensions:

r → ( t ) = x ( t ) i ^ + y ( t ) j ^ and v → ( t ) = v x ( t ) i ^ + v y ( t ) j ^ .

The following example illustrates a practical use of the kinematic equations in two dimensions.

A skier

[link] shows a skier moving with an acceleration of 2.1 m/ s 2 down a slope of 15 ° at t = 0. With the origin of the coordinate system at the front of the lodge, her initial position and velocity are

r → ( 0 ) = ( 75.0 i ^ − 50.0 j ^ ) m

and

v → ( 0 ) = ( 4.1 i ^ − 1.1 j ^ ) m/s .

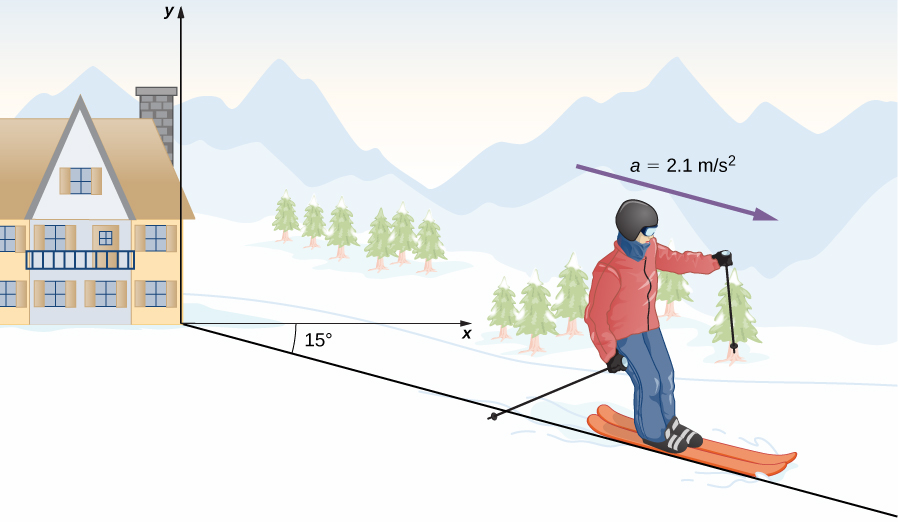
(a) What are the x- and y -components of the skier’s position and velocity as functions of time? (b) What are her position and velocity at t = 10.0 s?

An illustration of a skier in an x y coordinate system is shown. The skier is moving along a line that is 15 degrees below the horizontal x direction and has an acceleration of a = 2.1 meters per second squared also directed in his direction of motion. The acceleration is represented as a purple arrow.
A skier has an acceleration of 2.1 m/s 2 down a slope of 15 ° . The origin of the coordinate system is at the ski lodge.

Strategy

Since we are evaluating the components of the motion equations in the x and y directions, we need to find the components of the acceleration and put them into the kinematic equations. The components of the acceleration are found by referring to the coordinate system in [link] . Then, by inserting the components of the initial position and velocity into the motion equations, we can solve for her position and velocity at a later time t .

Questions & Answers

how does Neisseria cause meningitis
Nyibol Reply
what is microbiologist
Muhammad Reply
what is errata
Muhammad
is the branch of biology that deals with the study of microorganisms.
Ntefuni Reply
What is microbiology
Mercy Reply
studies of microbes
Louisiaste
when we takee the specimen which lumbar,spin,
Ziyad Reply
How bacteria create energy to survive?
Muhamad Reply
Bacteria doesn't produce energy they are dependent upon their substrate in case of lack of nutrients they are able to make spores which helps them to sustain in harsh environments
_Adnan
But not all bacteria make spores, l mean Eukaryotic cells have Mitochondria which acts as powerhouse for them, since bacteria don't have it, what is the substitution for it?
Muhamad
they make spores
Louisiaste
what is sporadic nd endemic, epidemic
Aminu Reply
the significance of food webs for disease transmission
Abreham
food webs brings about an infection as an individual depends on number of diseased foods or carriers dully.
Mark
explain assimilatory nitrate reduction
Esinniobiwa Reply
Assimilatory nitrate reduction is a process that occurs in some microorganisms, such as bacteria and archaea, in which nitrate (NO3-) is reduced to nitrite (NO2-), and then further reduced to ammonia (NH3).
Elkana
This process is called assimilatory nitrate reduction because the nitrogen that is produced is incorporated in the cells of microorganisms where it can be used in the synthesis of amino acids and other nitrogen products
Elkana
Examples of thermophilic organisms
Shu Reply
Give Examples of thermophilic organisms
Shu
advantages of normal Flora to the host
Micheal Reply
Prevent foreign microbes to the host
Abubakar
they provide healthier benefits to their hosts
ayesha
They are friends to host only when Host immune system is strong and become enemies when the host immune system is weakened . very bad relationship!
Mark
what is cell
faisal Reply
cell is the smallest unit of life
Fauziya
cell is the smallest unit of life
Akanni
ok
Innocent
cell is the structural and functional unit of life
Hasan
is the fundamental units of Life
Musa
what are emergency diseases
Micheal Reply
There are nothing like emergency disease but there are some common medical emergency which can occur simultaneously like Bleeding,heart attack,Breathing difficulties,severe pain heart stock.Hope you will get my point .Have a nice day ❣️
_Adnan
define infection ,prevention and control
Innocent
I think infection prevention and control is the avoidance of all things we do that gives out break of infections and promotion of health practices that promote life
Lubega
Heyy Lubega hussein where are u from?
_Adnan
en français
Adama
which site have a normal flora
ESTHER Reply
Many sites of the body have it Skin Nasal cavity Oral cavity Gastro intestinal tract
Safaa
skin
Asiina
skin,Oral,Nasal,GIt
Sadik
How can Commensal can Bacteria change into pathogen?
Sadik
How can Commensal Bacteria change into pathogen?
Sadik
all
Tesfaye
by fussion
Asiina
what are the advantages of normal Flora to the host
Micheal
what are the ways of control and prevention of nosocomial infection in the hospital
Micheal
what is inflammation
Shelly Reply
part of a tissue or an organ being wounded or bruised.
Wilfred
what term is used to name and classify microorganisms?
Micheal Reply
Binomial nomenclature
adeolu
Got questions? Join the online conversation and get instant answers!
Jobilize.com Reply
<< Chapter < Page Page > Chapter >>
Practice Key Terms 1

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, University physics volume 1. OpenStax CNX. Sep 19, 2016 Download for free at http://cnx.org/content/col12031/1.5
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'University physics volume 1' conversation and receive update notifications?

Ask