| << Chapter < Page | Chapter >> Page > |
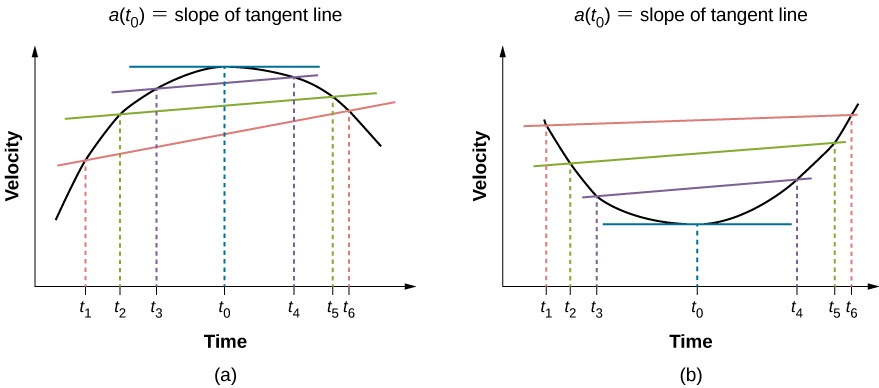
Thus, similar to velocity being the derivative of the position function, instantaneous acceleration is the derivative of the velocity function. We can show this graphically in the same way as instantaneous velocity. In [link] , instantaneous acceleration at time t 0 is the slope of the tangent line to the velocity-versus-time graph at time t 0 . We see that average acceleration approaches instantaneous acceleration as approaches zero. Also in part (a) of the figure, we see that velocity has a maximum when its slope is zero. This time corresponds to the zero of the acceleration function. In part (b), instantaneous acceleration at the minimum velocity is shown, which is also zero, since the slope of the curve is zero there, too. Thus, for a given velocity function, the zeros of the acceleration function give either the minimum or the maximum velocity.
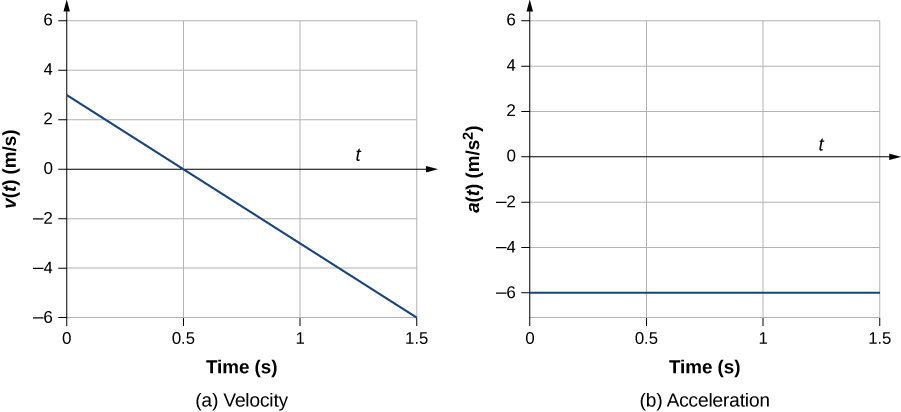
To illustrate this concept, let’s look at two examples. First, a simple example is shown using [link] (b), the velocity-versus-time graph of [link] , to find acceleration graphically. This graph is depicted in [link] (a), which is a straight line. The corresponding graph of acceleration versus time is found from the slope of velocity and is shown in [link] (b). In this example, the velocity function is a straight line with a constant slope, thus acceleration is a constant. In the next example, the velocity function is has a more complicated functional dependence on time.
If we know the functional form of velocity, v ( t ), we can calculate instantaneous acceleration a ( t ) at any time point in the motion using [link] .

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?