| << Chapter < Page | Chapter >> Page > |

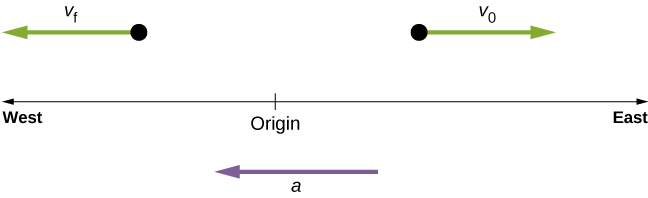
The term deceleration can cause confusion in our analysis because it is not a vector and it does not point to a specific direction with respect to a coordinate system, so we do not use it. Acceleration is a vector, so we must choose the appropriate sign for it in our chosen coordinate system. In the case of the train in [link] , acceleration is in the negative direction in the chosen coordinate system , so we say the train is undergoing negative acceleration.
If an object in motion has a velocity in the positive direction with respect to a chosen origin and it acquires a constant negative acceleration, the object eventually comes to a rest and reverses direction. If we wait long enough, the object passes through the origin going in the opposite direction. This is illustrated in [link] .


We can solve this problem by identifying from the given information, and then calculating the average acceleration directly from the equation .
Second, find the change in velocity. Since the horse is going from zero to –15.0 m/s, its change in velocity equals its final velocity:
Last, substitute the known values ( ) and solve for the unknown :
Check Your Understanding Protons in a linear accelerator are accelerated from rest to in 10 –4 s. What is the average acceleration of the protons?
Inserting the knowns, we have
Instantaneous acceleration a , or acceleration at a specific instant in time , is obtained using the same process discussed for instantaneous velocity. That is, we calculate the average velocity between two points in time separated by and let approach zero. The result is the derivative of the velocity function v ( t ), which is instantaneous acceleration and is expressed mathematically as

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?