| << Chapter < Page | Chapter >> Page > |
Newton’s law of gravitation can be expressed as
where is the force on object 1 exerted by object 2 and is a unit vector that points from object 1 toward object 2.
As shown in [link] , the vector points from object 1 toward object 2, and hence represents an attractive force between the objects. The equal but opposite force is the force on object 2 exerted by object 1.
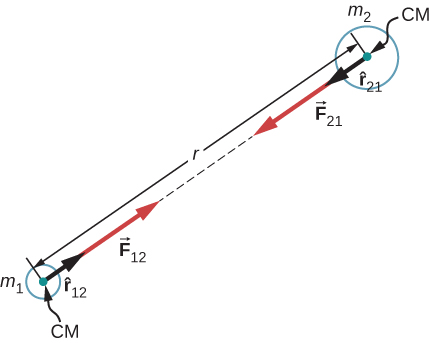
These equal but opposite forces reflect Newton’s third law, which we discussed earlier. Note that strictly speaking, [link] applies to point masses—all the mass is located at one point. But it applies equally to any spherically symmetric objects, where r is the distance between the centers of mass of those objects. In many cases, it works reasonably well for nonsymmetrical objects, if their separation is large compared to their size, and we take r to be the distance between the center of mass of each body.
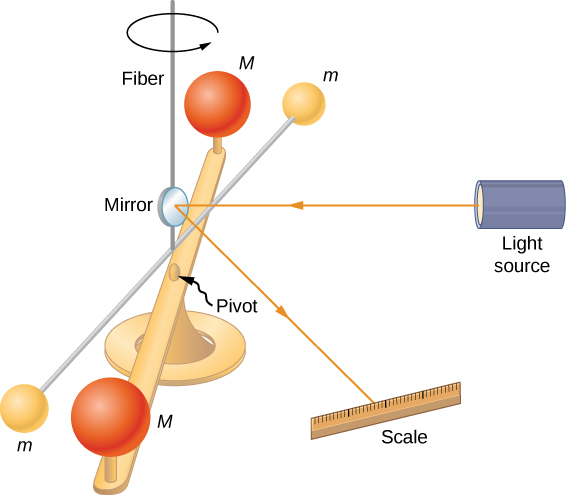
A century after Newton published his law of universal gravitation, Henry Cavendish determined the proportionality constant G by performing a painstaking experiment. He constructed a device similar to that shown in [link] , in which small masses are suspended from a wire. Once in equilibrium, two fixed, larger masses are placed symmetrically near the smaller ones. The gravitational attraction creates a torsion (twisting) in the supporting wire that can be measured.
The constant G is called the universal gravitational constant and Cavendish determined it to be . The word ‘universal’ indicates that scientists think that this constant applies to masses of any composition and that it is the same throughout the Universe. The value of G is an incredibly small number, showing that the force of gravity is very weak. The attraction between masses as small as our bodies, or even objects the size of skyscrapers, is incredibly small. For example, two 1.0-kg masses located 1.0 meter apart exert a force of on each other. This is the weight of a typical grain of pollen.
Although gravity is the weakest of the four fundamental forces of nature, its attractive nature is what holds us to Earth, causes the planets to orbit the Sun and the Sun to orbit our galaxy, and binds galaxies into clusters, ranging from a few to millions. Gravity is the force that forms the Universe.
To determine the motion caused by the gravitational force, follow these steps:

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?