12.2 Examples of static equilibrium  (Page 6/9)

Strategy

Solution

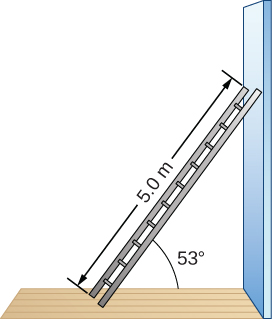
the net force in the y -direction is

and the net torque along the rotation axis at the pivot point is

where ${\tau }_w$ is the torque of the weight w and ${\tau }_F$ is the torque of the reaction F . From the free-body diagram, we identify that the lever arm of the reaction at the wall is $r_F=L=5.0\text{m}$ and the lever arm of the weight is $r_w=L\text{/}2=2.5\text{m}.$ With the help of the free-body diagram, we identify the angles to be used in [link] for torques: ${\theta }_F=180\text{°}-\beta$ for the torque from the reaction force with the wall, and ${\theta }_w=180\text{°}+(90\text{°}-\beta )$ for the torque due to the weight. Now we are ready to use [link] to compute torques:

We substitute the torques into [link] and solve for $F:$

We obtain the normal reaction force with the floor by solving [link] : $N=w=400.0\text{N}.$ The magnitude of friction is obtained by solving [link] : $f=F=150.7\text{N}.$ The coefficient of static friction is ${\mu }_{\text{s}}=f\text{/}N=150.7\text{/}400.0=0.377.$

The net force on the ladder at the contact point with the floor is the vector sum of the normal reaction from the floor and the static friction forces:

Its magnitude is

and its direction is

We should emphasize here two general observations of practical use. First, notice that when we choose a pivot point, there is no expectation that the system will actually pivot around the chosen point. The ladder in this example is not rotating at all but firmly stands on the floor; nonetheless, its contact point with the floor is a good choice for the pivot. Second, notice when we use [link] for the computation of individual torques, we do not need to resolve the forces into their normal and parallel components with respect to the direction of the lever arm, and we do not need to consider a sense of the torque. As long as the angle in [link] is correctly identified—with the help of a free-body diagram—as the angle measured counterclockwise from the direction of the lever arm to the direction of the force vector, [link] gives both the magnitude and the sense of the torque. This is because torque is the vector product of the lever-arm vector crossed with the force vector, and [link] expresses the rectangular component of this vector product along the axis of rotation.