| << Chapter < Page | Chapter >> Page > |
Also, in this example, the kinetic energy, or energy of motion, is equally shared between linear and rotational motion. If we look at the moments of inertia in [link] , we see that the hollow cylinder has the largest moment of inertia for a given radius and mass. If the wheels of the rover were solid and approximated by solid cylinders, for example, there would be more kinetic energy in linear motion than in rotational motion. This would give the wheel a larger linear velocity than the hollow cylinder approximation. Thus, the solid cylinder would reach the bottom of the basin faster than the hollow cylinder.
Can a round object released from rest at the top of a frictionless incline undergo rolling motion?
No, the static friction force is zero.
A cylindrical can of radius R is rolling across a horizontal surface without slipping. (a) After one complete revolution of the can, what is the distance that its center of mass has moved? (b) Would this distance be greater or smaller if slipping occurred?
A wheel is released from the top on an incline. Is the wheel most likely to slip if the incline is steep or gently sloped?
The wheel is more likely to slip on a steep incline since the coefficient of static friction must increase with the angle to keep rolling motion without slipping.
Which rolls down an inclined plane faster, a hollow cylinder or a solid sphere? Both have the same mass and radius.
A hollow sphere and a hollow cylinder of the same radius and mass roll up an incline without slipping and have the same initial center of mass velocity. Which object reaches a greater height before stopping?
The cylinder reaches a greater height. By [link] , its acceleration in the direction down the incline would be less.
What is the angular velocity of a 75.0-cm-diameter tire on an automobile traveling at 90.0 km/h?
A boy rides his bicycle 2.00 km. The wheels have radius 30.0 cm. What is the total angle the tires rotate through during his trip?
If the boy on the bicycle in the preceding problem accelerates from rest to a speed of 10.0 m/s in 10.0 s, what is the angular acceleration of the tires?
Formula One race cars have 66-cm-diameter tires. If a Formula One averages a speed of 300 km/h during a race, what is the angular displacement in revolutions of the wheels if the race car maintains this speed for 1.5 hours?
A marble rolls down an incline at from rest. (a) What is its acceleration? (b) How far does it go in 3.0 s?
Repeat the preceding problem replacing the marble with a solid cylinder. Explain the new result.
A rigid body with a cylindrical cross-section is released from the top of a incline. It rolls 10.0 m to the bottom in 2.60 s. Find the moment of inertia of the body in terms of its mass m and radius r.
positive is down the incline plane;
,
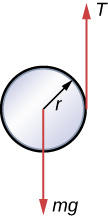
A yo-yo can be thought of a solid cylinder of mass m and radius r that has a light string wrapped around its circumference (see below). One end of the string is held fixed in space. If the cylinder falls as the string unwinds without slipping, what is the acceleration of the cylinder?
A solid cylinder of radius 10.0 cm rolls down an incline with slipping. The angle of the incline is The coefficient of kinetic friction on the surface is 0.400. What is the angular acceleration of the solid cylinder? What is the linear acceleration?
,
A bowling ball rolls up a ramp 0.5 m high without slipping to storage. It has an initial velocity of its center of mass of 3.0 m/s. (a) What is its velocity at the top of the ramp? (b) If the ramp is 1 m high does it make it to the top?
A 40.0-kg solid cylinder is rolling across a horizontal surface at a speed of 6.0 m/s. How much work is required to stop it?
A 40.0-kg solid sphere is rolling across a horizontal surface with a speed of 6.0 m/s. How much work is required to stop it? Compare results with the preceding problem.
A solid cylinder rolls up an incline at an angle of If it starts at the bottom with a speed of 10 m/s, how far up the incline does it travel?
Mechanical energy at the bottom equals mechanical energy at the top;
,
so the distance up the incline is
.
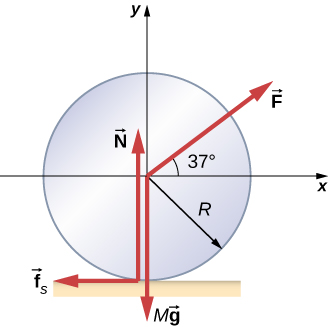
A solid cylindrical wheel of mass M and radius R is pulled by a force applied to the center of the wheel at to the horizontal (see the following figure). If the wheel is to roll without slipping, what is the maximum value of The coefficients of static and kinetic friction are
A hollow cylinder is given a velocity of 5.0 m/s and rolls up an incline to a height of 1.0 m. If a hollow sphere of the same mass and radius is given the same initial velocity, how high does it roll up the incline?
Use energy conservation
,
.
Subtracting the two equations, eliminating the initial translational energy, we have
,
,
,
.
Thus, the hollow sphere, with the smaller moment of inertia, rolls up to a lower height of

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?