10.1 Rotational variables  (Page 2/11)

where $\theta$ is the angle of rotation ( [link] ). The units of angular velocity are radians per second (rad/s). Angular velocity can also be referred to as the rotation rate in radians per second. In many situations, we are given the rotation rate in revolutions/s or cycles/s. To find the angular velocity, we must multiply revolutions/s by $2\pi$ , since there are $2\pi$ radians in one complete revolution. Since the direction of a positive angle in a circle is counterclockwise, we take counterclockwise rotations as being positive and clockwise rotations as negative.

We can see how angular velocity is related to the tangential speed of the particle by differentiating [link] with respect to time. We rewrite [link] as

Taking the derivative with respect to time and noting that the radius r is a constant, we have

where $\theta \frac{dr}{dt}=0$ . Here $\frac{ds}{dt}$ is just the tangential speed $v_{\text{t}}$ of the particle in [link] . Thus, by using [link] , we arrive at

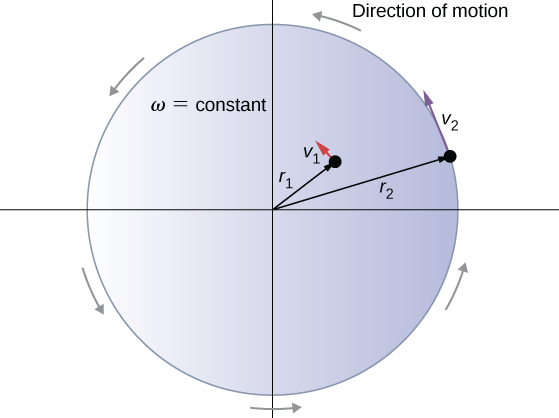
That is, the tangential speed of the particle is its angular velocity times the radius of the circle. From [link] , we see that the tangential speed of the particle increases with its distance from the axis of rotation for a constant angular velocity. This effect is shown in [link] . Two particles are placed at different radii on a rotating disk with a constant angular velocity. As the disk rotates, the tangential speed increases linearly with the radius from the axis of rotation. In [link] , we see that $v_1=r_1{\omega }_1$ and $v_2=r_2{\omega }_2$ . But the disk has a constant angular velocity, so ${\omega }_1={\omega }_2$ . This means $\frac{v_1}{r_1}=\frac{v_2}{r_2}$ or $v_2=\left(\frac{r_2}{r_1}\right)v_1$ . Thus, since $r_2>r_1$ , $v_2>v_1$ .

Up until now, we have discussed the magnitude of the angular velocity $\omega =d\theta \text{/}dt,$ which is a scalar quantity—the change in angular position with respect to time. The vector $\overrightarrow{\omega }$ is the vector associated with the angular velocity and points along the axis of rotation. This is useful because when a rigid body is rotating, we want to know both the axis of rotation and the direction that the body is rotating about the axis, clockwise or counterclockwise. The angular velocity $\overrightarrow{\omega }$ gives us this information. The angular velocity $\overrightarrow{\omega }$ has a direction determined by what is called the right-hand rule. The right-hand rule is such that if the fingers of your right hand wrap counterclockwise from the x -axis (the direction in which $\theta$ increases) toward the y- axis, your thumb points in the direction of the positive z -axis ( [link] ). An angular velocity $\overrightarrow{\omega }$ that points along the positive z -axis therefore corresponds to a counterclockwise rotation, whereas an angular velocity $\overrightarrow{\omega }$ that points along the negative z -axis corresponds to a clockwise rotation.

We can verify the right-hand-rule using the vector expression for the arc length $\overrightarrow{s}=\overrightarrow{\theta }\times \overrightarrow{r}$ , [link] . If we differentiate this equation with respect to time, we find