| << Chapter < Page | Chapter >> Page > |
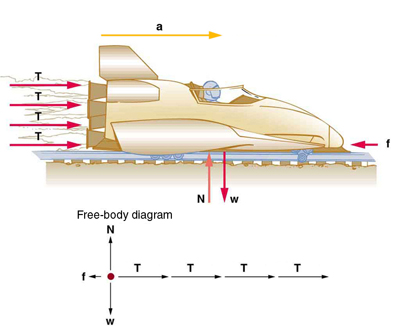
Prior to manned space flights, rocket sleds were used to test aircraft, missile equipment, and physiological effects on human subjects at high speeds. They consisted of a platform that was mounted on one or two rails and propelled by several rockets. Calculate the magnitude of force exerted by each rocket, called its thrust , for the four-rocket propulsion system shown in [link] . The sled’s initial acceleration is the mass of the system is 2100 kg, and the force of friction opposing the motion is known to be 650 N.
Strategy
Although there are forces acting vertically and horizontally, we assume the vertical forces cancel since there is no vertical acceleration. This leaves us with only horizontal forces and a simpler one-dimensional problem. Directions are indicated with plus or minus signs, with right taken as the positive direction. See the free-body diagram in the figure.
Solution
Since acceleration, mass, and the force of friction are given, we start with Newton’s second law and look for ways to find the thrust of the engines. Since we have defined the direction of the force and acceleration as acting “to the right,” we need to consider only the magnitudes of these quantities in the calculations. Hence we begin with
where is the net force along the horizontal direction. We can see from [link] that the engine thrusts add, while friction opposes the thrust. In equation form, the net external force is
Substituting this into Newton’s second law gives
Using a little algebra, we solve for the total thrust 4 T :
Substituting known values yields
So the total thrust is
and the individual thrusts are
Discussion
The numbers are quite large, so the result might surprise you. Experiments such as this were performed in the early 1960s to test the limits of human endurance and the setup designed to protect human subjects in jet fighter emergency ejections. Speeds of 1000 km/h were obtained, with accelerations of 45 's. (Recall that , the acceleration due to gravity, is . When we say that an acceleration is 45 's, it is , which is approximately .) While living subjects are not used any more, land speeds of 10,000 km/h have been obtained with rocket sleds. In this example, as in the preceding one, the system of interest is obvious. We will see in later examples that choosing the system of interest is crucial—and the choice is not always obvious.

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?