| << Chapter < Page | Chapter >> Page > |
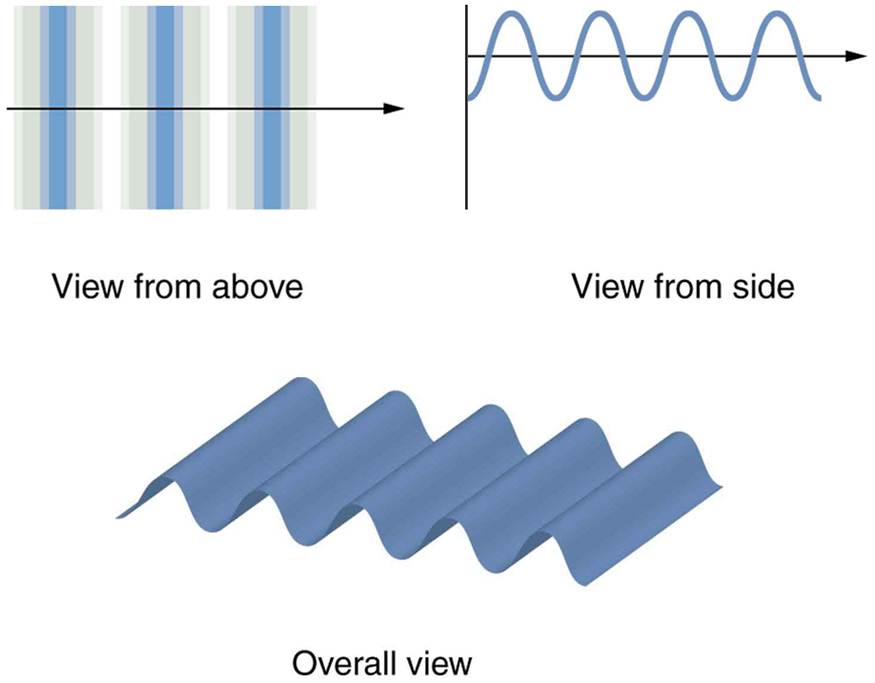
[link] shows how a transverse wave looks as viewed from above and from the side. A light wave can be imagined to propagate like this, although we do not actually see it wiggling through space. From above, we view the wavefronts (or wave crests) as we would by looking down on the ocean waves. The side view would be a graph of the electric or magnetic field. The view from above is perhaps the most useful in developing concepts about wave optics.
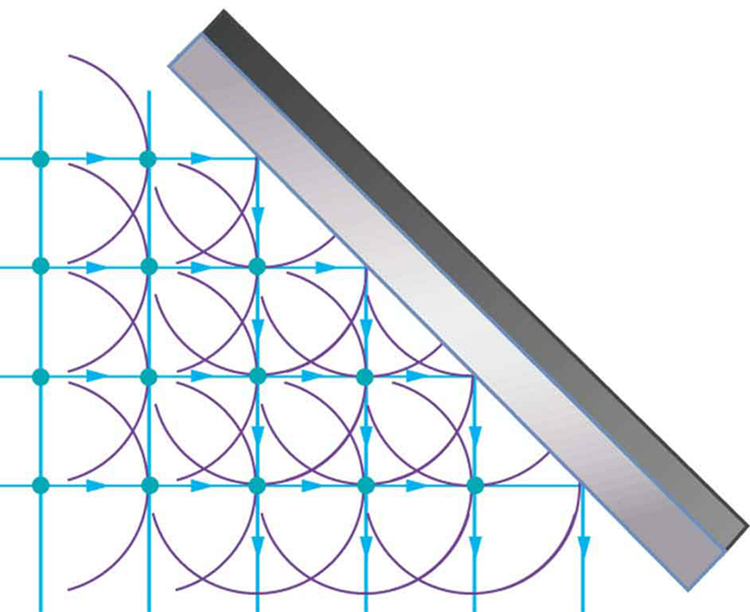
The Dutch scientist Christiaan Huygens (1629–1695) developed a useful technique for determining in detail how and where waves propagate. Starting from some known position, Huygens’s principle states that:
Every point on a wavefront is a source of wavelets that spread out in the forward direction at the same speed as the wave itself. The new wavefront is a line tangent to all of the wavelets.
[link] shows how Huygens’s principle is applied. A wavefront is the long edge that moves, for example, the crest or the trough. Each point on the wavefront emits a semicircular wave that moves at the propagation speed . These are drawn at a time later, so that they have moved a distance . The new wavefront is a line tangent to the wavelets and is where we would expect the wave to be a time later. Huygens’s principle works for all types of waves, including water waves, sound waves, and light waves. We will find it useful not only in describing how light waves propagate, but also in explaining the laws of reflection and refraction. In addition, we will see that Huygens’s principle tells us how and where light rays interfere.

[link] shows how a mirror reflects an incoming wave at an angle equal to the incident angle, verifying the law of reflection. As the wavefront strikes the mirror, wavelets are first emitted from the left part of the mirror and then the right. The wavelets closer to the left have had time to travel farther, producing a wavefront traveling in the direction shown.
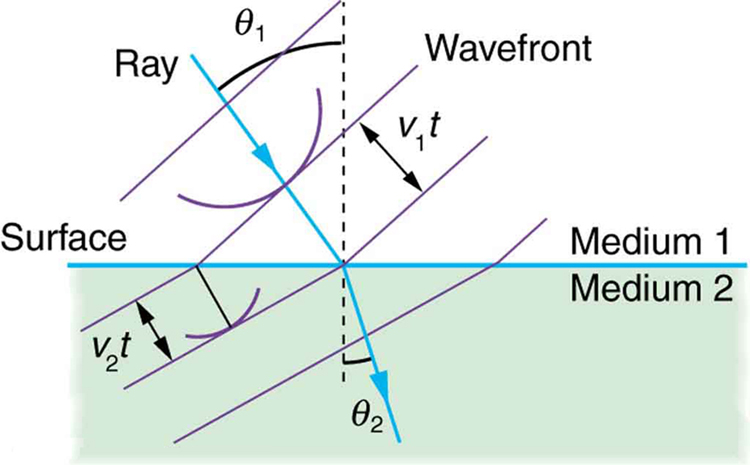
The law of refraction can be explained by applying Huygens’s principle to a wavefront passing from one medium to another (see [link] ). Each wavelet in the figure was emitted when the wavefront crossed the interface between the media. Since the speed of light is smaller in the second medium, the waves do not travel as far in a given time, and the new wavefront changes direction as shown. This explains why a ray changes direction to become closer to the perpendicular when light slows down. Snell’s law can be derived from the geometry in [link] , but this is left as an exercise for ambitious readers.
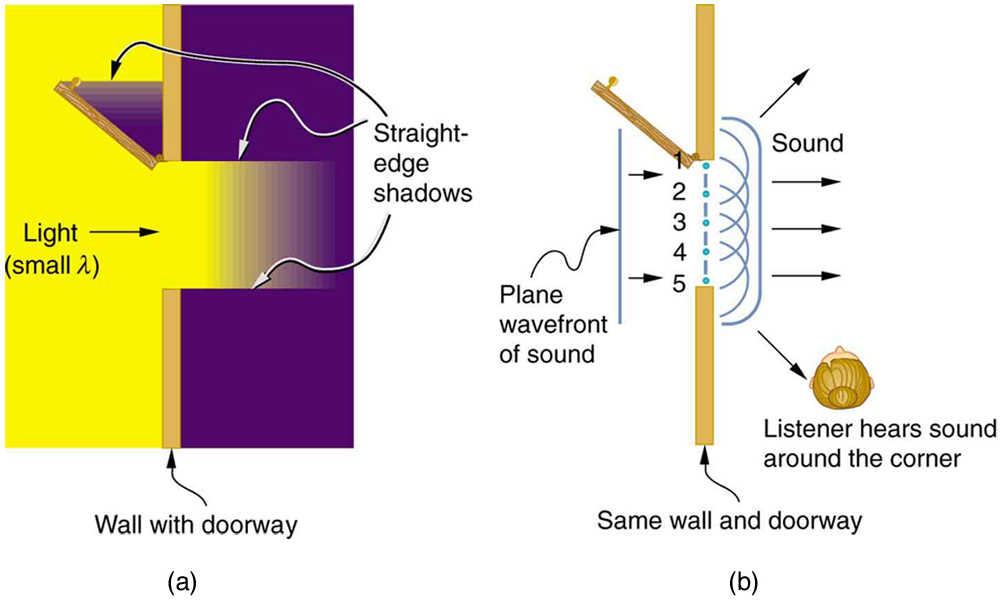
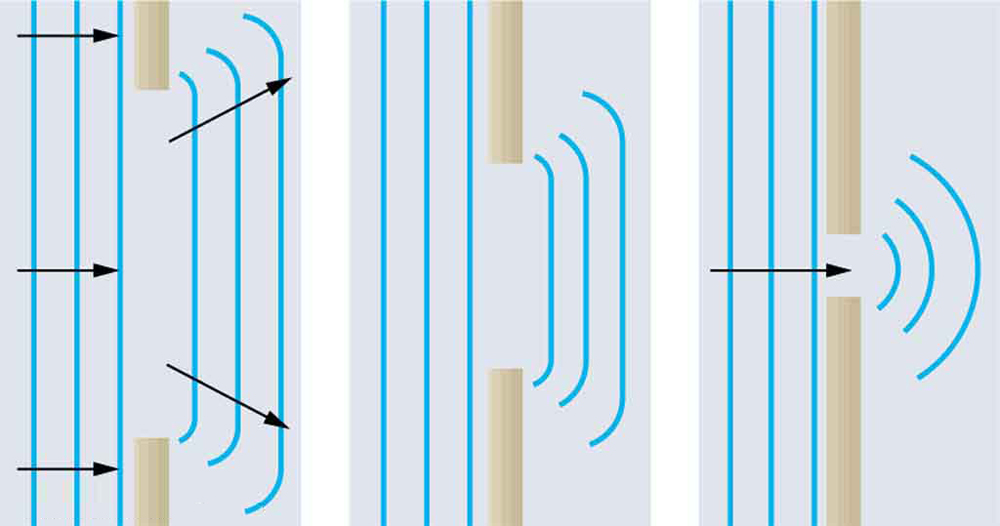
What happens when a wave passes through an opening, such as light shining through an open door into a dark room? For light, we expect to see a sharp shadow of the doorway on the floor of the room, and we expect no light to bend around corners into other parts of the room. When sound passes through a door, we expect to hear it everywhere in the room and, thus, expect that sound spreads out when passing through such an opening (see [link] ). What is the difference between the behavior of sound waves and light waves in this case? The answer is that light has very short wavelengths and acts like a ray. Sound has wavelengths on the order of the size of the door and bends around corners (for frequency of 1000 Hz, , about three times smaller than the width of the doorway).
If we pass light through smaller openings, often called slits, we can use Huygens’s principle to see that light bends as sound does (see [link] ). The bending of a wave around the edges of an opening or an obstacle is called diffraction . Diffraction is a wave characteristic and occurs for all types of waves. If diffraction is observed for some phenomenon, it is evidence that the phenomenon is a wave. Thus the horizontal diffraction of the laser beam after it passes through slits in [link] is evidence that light is a wave.
How do wave effects depend on the size of the object with which the wave interacts? For example, why does sound bend around the corner of a building while light does not?
Under what conditions can light be modeled like a ray? Like a wave?
Go outside in the sunlight and observe your shadow. It has fuzzy edges even if you do not. Is this a diffraction effect? Explain.
Why does the wavelength of light decrease when it passes from vacuum into a medium? State which attributes change and which stay the same and, thus, require the wavelength to decrease.
Does Huygens’s principle apply to all types of waves?

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?