| << Chapter < Page | Chapter >> Page > |
A manned rocket accelerates at a rate of during launch. How long does it take the rocket to reach a velocity of 400 m/s?
To answer this, choose an equation that allows you to solve for time , given only , , and .
Rearrange to solve for .
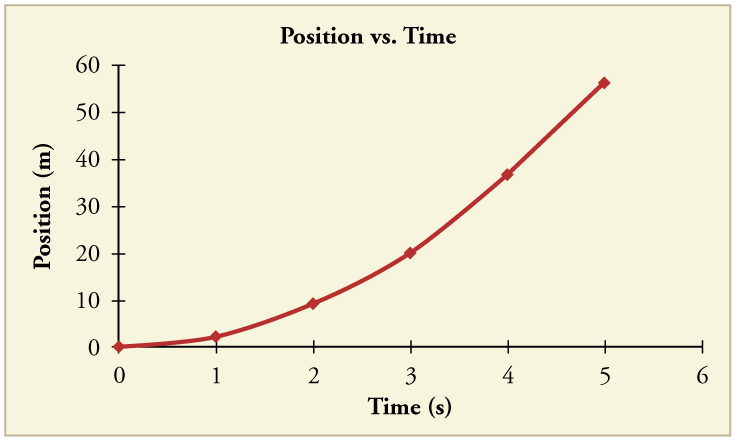
An Olympic-class sprinter starts a race with an acceleration of . (a) What is her speed 2.40 s later? (b) Sketch a graph of her position vs. time for this period.
(a)
(b)
A well-thrown ball is caught in a well-padded mitt. If the deceleration of the ball is , and 1.85 ms elapses from the time the ball first touches the mitt until it stops, what was the initial velocity of the ball?
38.9 m/s (about 87 miles per hour)
A bullet in a gun is accelerated from the firing chamber to the end of the barrel at an average rate of for . What is its muzzle velocity (that is, its final velocity)?
(a) A light-rail commuter train accelerates at a rate of . How long does it take to reach its top speed of 80.0 km/h, starting from rest? (b) The same train ordinarily decelerates at a rate of . How long does it take to come to a stop from its top speed? (c) In emergencies the train can decelerate more rapidly, coming to rest from 80.0 km/h in 8.30 s. What is its emergency deceleration in ?
(a)
(b)
(c)
While entering a freeway, a car accelerates from rest at a rate of for 12.0 s. (a) Draw a sketch of the situation. (b) List the knowns in this problem. (c) How far does the car travel in those 12.0 s? To solve this part, first identify the unknown, and then discuss how you chose the appropriate equation to solve for it. After choosing the equation, show your steps in solving for the unknown, check your units, and discuss whether the answer is reasonable. (d) What is the car’s final velocity? Solve for this unknown in the same manner as in part (c), showing all steps explicitly.
At the end of a race, a runner decelerates from a velocity of 9.00 m/s at a rate of . (a) How far does she travel in the next 5.00 s? (b) What is her final velocity? (c) Evaluate the result. Does it make sense?
(a)
(b)
(c) This result does not really make sense. If the runner starts at 9.00 m/s and decelerates at , then she will have stopped after 4.50 s. If she continues to decelerate, she will be running backwards.
Professional Application:
Blood is accelerated from rest to 30.0 cm/s in a distance of 1.80 cm by the left ventricle of the heart. (a) Make a sketch of the situation. (b) List the knowns in this problem. (c) How long does the acceleration take? To solve this part, first identify the unknown, and then discuss how you chose the appropriate equation to solve for it. After choosing the equation, show your steps in solving for the unknown, checking your units. (d) Is the answer reasonable when compared with the time for a heartbeat?

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?