| << Chapter < Page | Chapter >> Page > |
A solenoid is a long coil of wire (with many turns or loops, as opposed to a flat loop). Because of its shape, the field inside a solenoid can be very uniform, and also very strong. The field just outside the coils is nearly zero. [link] shows how the field looks and how its direction is given by RHR-2.
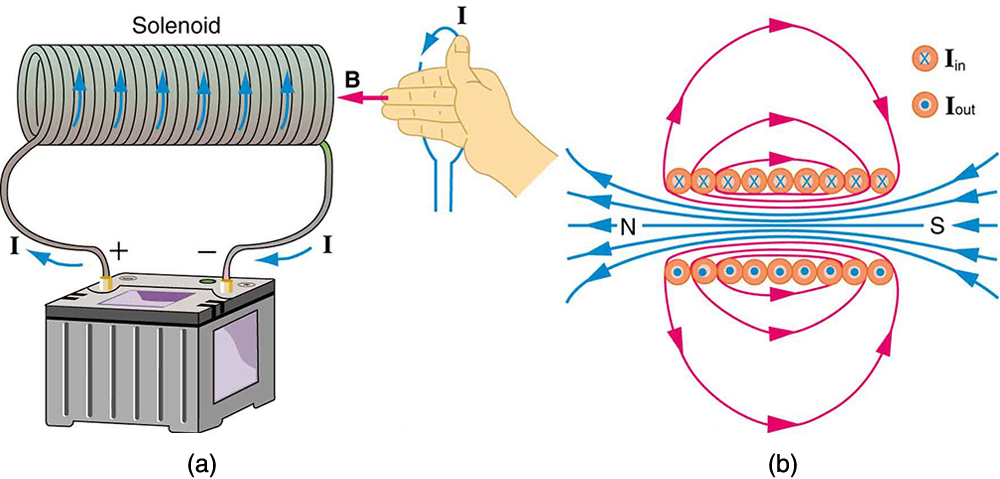
The magnetic field inside of a current-carrying solenoid is very uniform in direction and magnitude. Only near the ends does it begin to weaken and change direction. The field outside has similar complexities to flat loops and bar magnets, but the magnetic field strength inside a solenoid is simply
where is the number of loops per unit length of the solenoid , with being the number of loops and the length). Note that is the field strength anywhere in the uniform region of the interior and not just at the center. Large uniform fields spread over a large volume are possible with solenoids, as [link] implies.
What is the field inside a 2.00-m-long solenoid that has 2000 loops and carries a 1600-A current?
Strategy
To find the field strength inside a solenoid, we use . First, we note the number of loops per unit length is
Solution
Substituting known values gives
Discussion
This is a large field strength that could be established over a large-diameter solenoid, such as in medical uses of magnetic resonance imaging (MRI). The very large current is an indication that the fields of this strength are not easily achieved, however. Such a large current through 1000 loops squeezed into a meter’s length would produce significant heating. Higher currents can be achieved by using superconducting wires, although this is expensive. There is an upper limit to the current, since the superconducting state is disrupted by very large magnetic fields.
There are interesting variations of the flat coil and solenoid. For example, the toroidal coil used to confine the reactive particles in tokamaks is much like a solenoid bent into a circle. The field inside a toroid is very strong but circular. Charged particles travel in circles, following the field lines, and collide with one another, perhaps inducing fusion. But the charged particles do not cross field lines and escape the toroid. A whole range of coil shapes are used to produce all sorts of magnetic field shapes. Adding ferromagnetic materials produces greater field strengths and can have a significant effect on the shape of the field. Ferromagnetic materials tend to trap magnetic fields (the field lines bend into the ferromagnetic material, leaving weaker fields outside it) and are used as shields for devices that are adversely affected by magnetic fields, including the Earth’s magnetic field.
Generate electricity with a bar magnet! Discover the physics behind the phenomena by exploring magnets and how you can use them to make a bulb light.

Make a drawing and use RHR-2 to find the direction of the magnetic field of a current loop in a motor (such as in [link] ). Then show that the direction of the torque on the loop is the same as produced by like poles repelling and unlike poles attracting.

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?