| << Chapter < Page | Chapter >> Page > |
Why are the forces exerted on the outside world by the limbs of our bodies usually much smaller than the forces exerted by muscles inside the body?
Explain why the forces in our joints are several times larger than the forces we exert on the outside world with our limbs. Can these forces be even greater than muscle forces?
Certain types of dinosaurs were bipedal (walked on two legs). What is a good reason that these creatures invariably had long tails if they had long necks?
Swimmers and athletes during competition need to go through certain postures at the beginning of the race. Consider the balance of the person and why start-offs are so important for races.
If the maximum force the biceps muscle can exert is 1000 N, can we pick up an object that weighs 1000 N? Explain your answer.
Suppose the biceps muscle was attached through tendons to the upper arm close to the elbow and the forearm near the wrist. What would be the advantages and disadvantages of this type of construction for the motion of the arm?
Explain one of the reasons why pregnant women often suffer from back strain late in their pregnancy.
Verify that the force in the elbow joint in [link] is 407 N, as stated in the text.
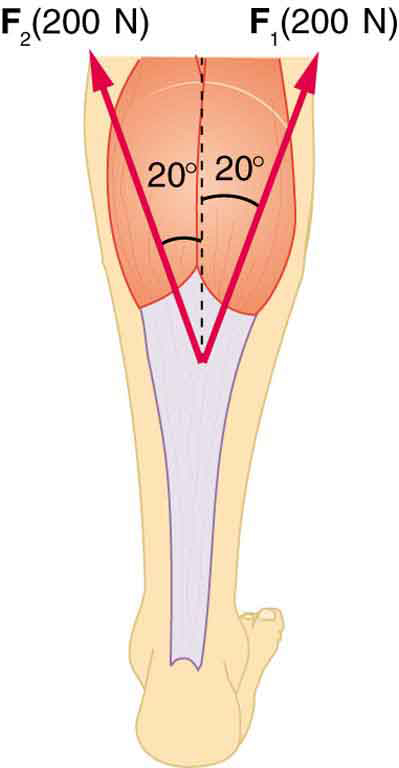
Two muscles in the back of the leg pull on the Achilles tendon as shown in [link] . What total force do they exert?
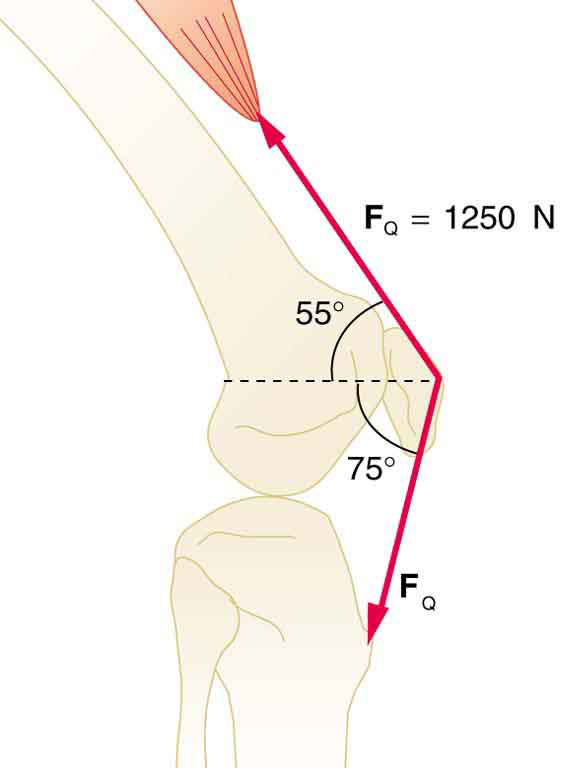
The upper leg muscle (quadriceps) exerts a force of 1250 N, which is carried by a tendon over the kneecap (the patella) at the angles shown in [link] . Find the direction and magnitude of the force exerted by the kneecap on the upper leg bone (the femur).
A device for exercising the upper leg muscle is shown in [link] , together with a schematic representation of an equivalent lever system. Calculate the force exerted by the upper leg muscle to lift the mass at a constant speed. Explicitly show how you follow the steps in the Problem-Solving Strategy for static equilibrium in Applications of Statistics, Including Problem-Solving Strategies .

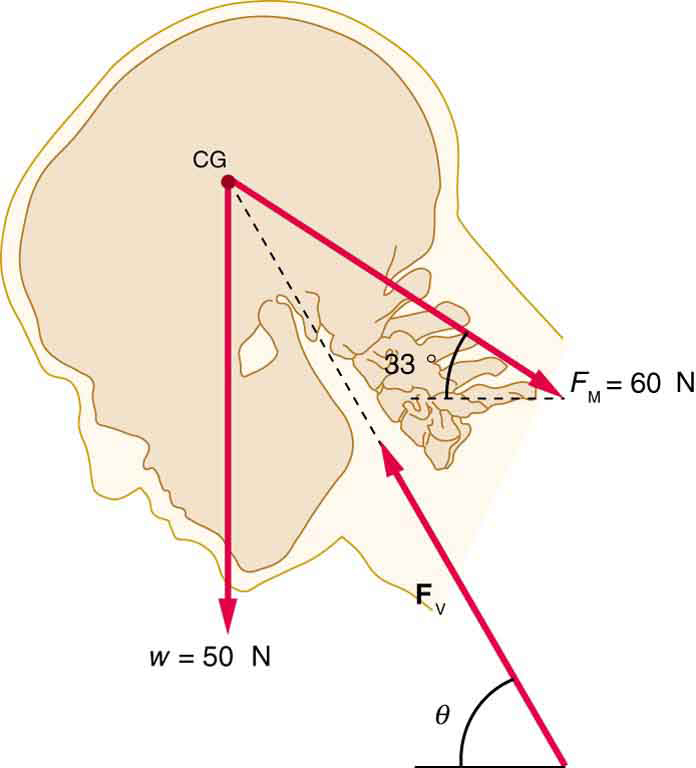
A person working at a drafting board may hold her head as shown in [link] , requiring muscle action to support the head. The three major acting forces are shown. Calculate the direction and magnitude of the force supplied by the upper vertebrae to hold the head stationary, assuming that this force acts along a line through the center of mass as do the weight and muscle force.

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?