| << Chapter < Page | Chapter >> Page > |
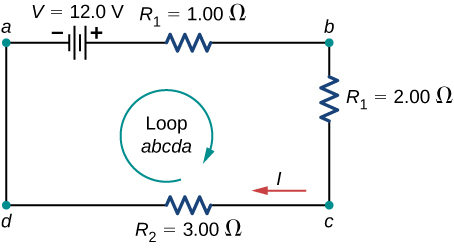
The circuit consists of a voltage source and three external load resistors. The labels a , b , c , and d serve as references, and have no other significance. The usefulness of these labels will become apparent soon. The loop is designated as Loop abcda , and the labels help keep track of the voltage differences as we travel around the circuit. Start at point a and travel to point b . The voltage of the voltage source is added to the equation and the potential drop of the resistor is subtracted. From point b to c , the potential drop across is subtracted. From c to d , the potential drop across is subtracted. From points d to a , nothing is done because there are no components.
[link] shows a graph of the voltage as we travel around the loop. Voltage increases as we cross the battery, whereas voltage decreases as we travel across a resistor. The potential drop , or change in the electric potential, is equal to the current through the resistor times the resistance of the resistor. Since the wires have negligible resistance, the voltage remains constant as we cross the wires connecting the components.

Then Kirchhoff’s loop rule states
The loop equation can be used to find the current through the loop:
This loop could have been analyzed using the previous methods, but we will demonstrate the power of Kirchhoff’s method in the next section.
By applying Kirchhoff’s rules, we generate a set of linear equations that allow us to find the unknown values in circuits. These may be currents, voltages, or resistances. Each time a rule is applied, it produces an equation. If there are as many independent equations as unknowns, then the problem can be solved.
Using Kirchhoff’s method of analysis requires several steps, as listed in the following procedure.

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?