| << Chapter < Page | Chapter >> Page > |
Why are the chemicals able to produce a unique potential difference? Quantum mechanical descriptions of molecules, which take into account the types of atoms and numbers of electrons in them, are able to predict the energy states they can have and the energies of reactions between them.
In the case of a lead-acid battery, an energy of 2 eV is given to each electron sent to the anode. Voltage is defined as the electrical potential energy divided by charge: . An electron volt is the energy given to a single electron by a voltage of 1 V. So the voltage here is 2 V, since 2 eV is given to each electron. It is the energy produced in each molecular reaction that produces the voltage. A different reaction produces a different energy and, hence, a different voltage.
The voltage output of a device is measured across its terminals and, thus, is called its terminal voltage . Terminal voltage is given by
where is the internal resistance and is the current flowing at the time of the measurement.
is positive if current flows away from the positive terminal, as shown in [link] . You can see that the larger the current, the smaller the terminal voltage. And it is likewise true that the larger the internal resistance, the smaller the terminal voltage.
Suppose a load resistance is connected to a voltage source, as in [link] . Since the resistances are in series, the total resistance in the circuit is . Thus the current is given by Ohm’s law to be
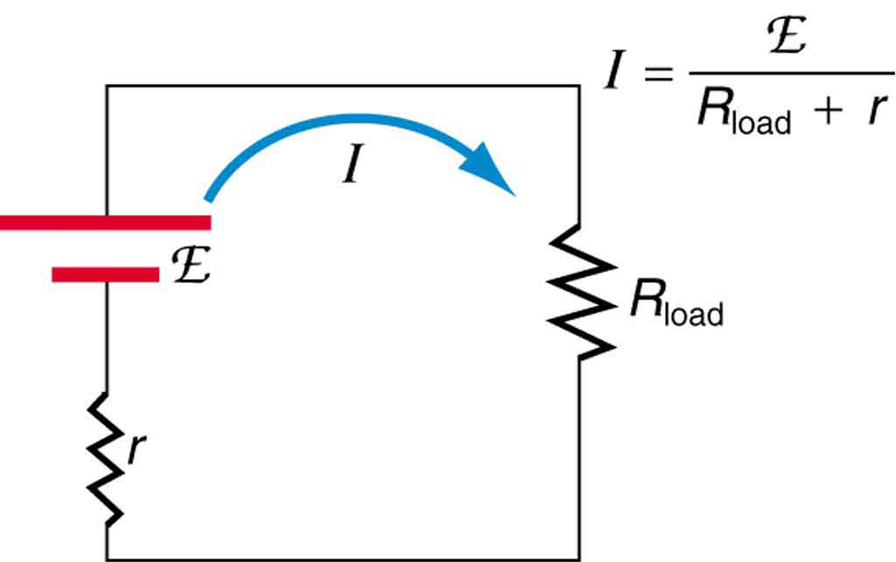
We see from this expression that the smaller the internal resistance , the greater the current the voltage source supplies to its load . As batteries are depleted, increases. If becomes a significant fraction of the load resistance, then the current is significantly reduced, as the following example illustrates.
A certain battery has a 12.0-V emf and an internal resistance of . (a) Calculate its terminal voltage when connected to a load. (b) What is the terminal voltage when connected to a load? (c) What power does the load dissipate? (d) If the internal resistance grows to , find the current, terminal voltage, and power dissipated by a load.
Strategy
The analysis above gave an expression for current when internal resistance is taken into account. Once the current is found, the terminal voltage can be calculated using the equation . Once current is found, the power dissipated by a resistor can also be found.
Solution for (a)
Entering the given values for the emf, load resistance, and internal resistance into the expression above yields
Enter the known values into the equation to get the terminal voltage:

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?