| << Chapter < Page | Chapter >> Page > |
Surface tension is proportional to the strength of the cohesive force, which varies with the type of liquid. Surface tension is defined to be the force F per unit length exerted by a stretched liquid membrane:
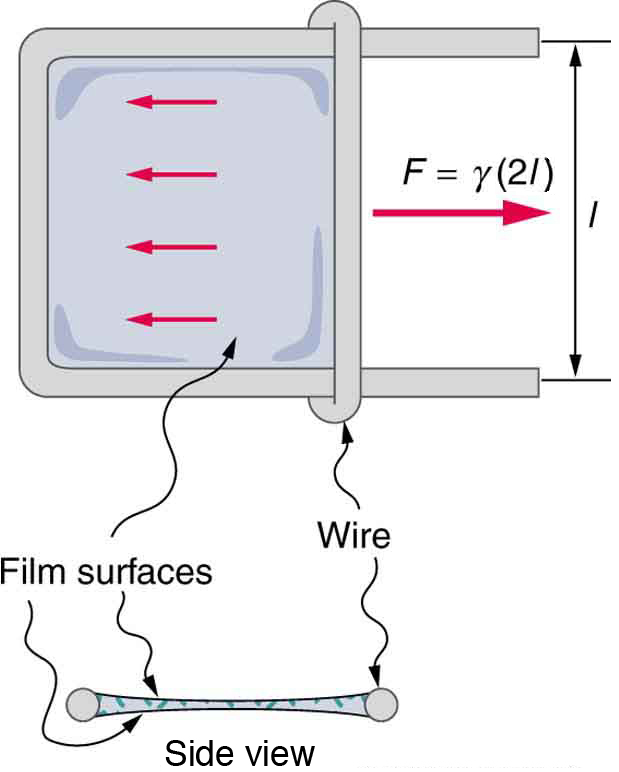
[link] lists values of for some liquids. For the insect of [link] (a), its weight is supported by the upward components of the surface tension force: , where is the circumference of the insect’s foot in contact with the water. [link] shows one way to measure surface tension. The liquid film exerts a force on the movable wire in an attempt to reduce its surface area. The magnitude of this force depends on the surface tension of the liquid and can be measured accurately.
Surface tension is the reason why liquids form bubbles and droplets. The inward surface tension force causes bubbles to be approximately spherical and raises the pressure of the gas trapped inside relative to atmospheric pressure outside. It can be shown that the gauge pressure inside a spherical bubble is given by
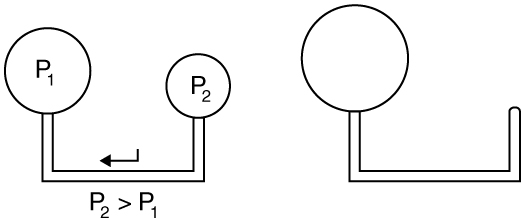
where is the radius of the bubble. Thus the pressure inside a bubble is greatest when the bubble is the smallest. Another bit of evidence for this is illustrated in [link] . When air is allowed to flow between two balloons of unequal size, the smaller balloon tends to collapse, filling the larger balloon.
| Liquid | Surface tension γ(N/m) |
|---|---|
| Water at | 0.0756 |
| Water at | 0.0728 |
| Water at | 0.0589 |
| Soapy water (typical) | 0.0370 |
| Ethyl alcohol | 0.0223 |
| Glycerin | 0.0631 |
| Mercury | 0.465 |
| Olive oil | 0.032 |
| Tissue fluids (typical) | 0.050 |
| Blood, whole at | 0.058 |
| Blood plasma at | 0.073 |
| Gold at | 1.000 |
| Oxygen at | 0.0157 |
| Helium at | 0.00012 |
Calculate the gauge pressure inside a soap bubble in radius using the surface tension for soapy water in [link] . Convert this pressure to mm Hg.
Strategy
The radius is given and the surface tension can be found in [link] , and so can be found directly from the equation .
Solution
Substituting and into the equation , we obtain
We use a conversion factor to get this into units of mm Hg:
Discussion
Note that if a hole were to be made in the bubble, the air would be forced out, the bubble would decrease in radius, and the pressure inside would increase to atmospheric pressure (760 mm Hg).

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?