| << Chapter < Page | Chapter >> Page > |
Problem : A circular disk of radius “R” rolls with constant angular velocity, “ω”, along a straight line. At an instant, the contact point of a rolling disk coincides with the origin of the coordinate system. Find the velocity of a particle, situated at a point (0,3R/2), as seen by (i) an observer on the ground (ii) an observer who is translating in the direction of rolling with a velocity “ωR/2” and (iii) an observer who is translating in the direction of rolling with a velocity equal to that of center of mass.
Velocity of a particle
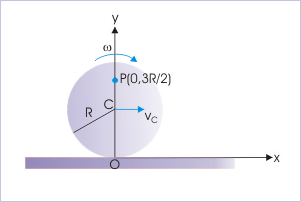
Solution : (i) The linear distance of the particle from the contact point is 3R/2. Since, particle is situated on the vertical diameter, the tangent to the circular path is horizontal. This means that particle is moving in horizontal direction (x – direction) with this speed. Hence, velocity of the particle as seen from the ground is :
(ii) The observer is moving with velocity “ωR/2” in the direction of rolling. Thus, relative velocity of the particle with respect to observer is :
(iii) The observer is moving with velocity of center of mass “ωR” in the direction of rolling. Thus, relative velocity of the particle with respect to observer is :
Note that the observer moving with the velocity of center of mass views rolling as pure rotation. The motion of the particle will be seen by the observer as the pure rotation of the particle about the perpendicular axis, which passes through center of mass. Now, particle is at a distance "3R/2 - R = R/2" from the central axis. Hence, linear velocity due to pure rotation only is :
Thus, the result is same as obtained when we consider rolling as pure rotation about instantaneous axis of rotation at contact point.
Example 4
Problem : A circular disk of radius “R” rolls with constant angular velocity, “ω”, along a straight line. At an instant, the contact point of a rolling disk coincides with the origin of the coordinate system. Find the velocity of a particle, situated at a point (R/2,3R/2), as seen by (i) an observer on the ground and (ii) an observer, who is translating in the direction of rolling with a velocity equal to that of center of mass.
Velocity of a particle

Solution : (i) In this case, velocity of the particle can be easily found out applying vector form of the relation,
Here, angular velocity is into the plane of disk and is, therefore, negative :
The position vector of the particle at the given instant is :
Hence, velocity of the particle is :
It is significant to note that signs of the components involved in the result is consistent with the physical interpretation as shown in the figure.
Velocity of a particle

(ii) The observer moving with the velocity of center of mass in the x-direction. Its velocity is :
Thus, relative velocity of the particle with respect to observer is :
Example 5
Problem : Find the distance covered in one complete revolution by a particle on the rim of a circular disk, which is rolling with constant velocity along a straight line on a horizontal plane.
Solution : The question, here, seeks to find the distance covered. We know that each particle on the rim of the disk moves along a cycloid curve as shown in the figure.
Path of a particle in rolling motion

The speed of the particle along the curve is not constant, but varies as :
where “θ” is the angle that the particle makes with vertical at the center. During one rotation, the angle varies from 0° to 360°. For this range of values, sin θ/2 varies between 0 to 1 in the first half and then 1 to 0 in the second half of the motion. The plot of speed – time approximates as shown here.
Speed – time plot

The differential distance covered is given as :
We know that the the area under speed – time curve gives the distance covered by the particle. Hence, distance is :
Speed – time plot

In order to have only one variable in the integration, we use the relation,
Substituting in the integration,
Putting the appropriate limits of time for one revolution and taking out the constants from the integration,
Example 6
Problem : A hollow sphere of mass “M” and radius “R” is rolling with a constant velocity “v”. What is ratio of translational kinetic energy and total kinetic energy.
Solution : The kinetic energy of the rolling sphere is given by :
Here,
and
For hollow sphere,
Putting these values in the equation of kinetic energy, we have :
The translational kinetic energy of the rigid body is given by :
Hence, the required ratio is :

Notification Switch
Would you like to follow the 'Physics for k-12' conversation and receive update notifications?