| << Chapter < Page | Chapter >> Page > |
As a matter of fact, there exists one to one correspondence between two types of equation sets. Importantly, we can treat angular vector quantities as signed scalars in the equations of motion, dispensing with the need to use vector notation. The similarity of situation suggests that we need not derive equations of motion again for the circular motion. We, therefore, proceed to simply write equation of angular motion with appropriate substitution.
The correspondence goes like this : the angular position is “θ” for linear “x”; the angular displacement is “Δθ” for linear “Δx”; the angular velocity is “ω” for linear “v” and the angular acceleration is “α” for linear “a”.
The different angular quantities corresponding to their linear counterparts are listed here fore ready reference :
The corresponding equations for the two types of motion are :
The derived equations for the two types of motion are :
The sign of angular quantities represents direction. A positive sign indicates anti-clockwise direction, whereas a negative sign indicates clockwise direction.
In the measurement of angle, a typical problem arises from the fact that circular motion may continue to rotate passing through the reference point again and again. The question arises, whether we keep adding angle or reset the measurement from the reference point ? The answer is that angle measurement is not reset in rotational kinematics. This means that we can have measurements like 540° and 20 rad etc.
Measurement of angle
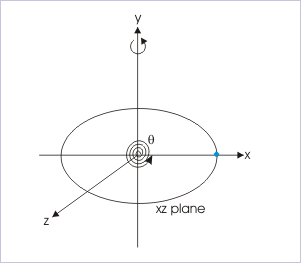
This convention is not without reason. Equations of motion of circular motion with constant acceleration treats motion in an equivalent linear frame work, which considers only one reference position. If we reset the measurements, then equations of motion would not be valid.
Problem : The angular velocity – time plot of the circular motion is shown in the figure. (i) Determine the nature of angular velocity and acceleration at positions marked A, B, C, D and E. (ii) In which of the segments (AB, BC, CD and DE) of motion, the particle is decelerated and (iii) Is angular acceleration constant during the motion ?
Angular velocity – time plot

Solution :
(i) Angular velocity :
The angular velocities at A and E are positive (anti-clockwise). The angular velocities at B and D are each zero. The angular velocities at C is negative (clockwise).
Angular acceleration :
The angular acceleration is equal to the first differential of angular velocity with respect to time.
The sign of the angular acceleration is determined by the sign of the slope at different positions. The slopes at various points are as shown in the figure :
Slopes at different points

The angular accelerations at point A and B are negative (angular speed decreases with the passage of time). The angular accelerations at C is zero. The angular accelerations at point D and E are positive (angular speed increases with the passage of time).
(ii) Deceleration :
In the segments AB and CD, the magnitude of angular velocity i.e. angular speed decreases with the passage of time. Thus, circular motions in these two segments are decelerated. This is also confirmed by the fact that angular velocity and angular acceleration are in opposite directions in these segments.
(iii) The slopes on angular velocity - time plot are different at different points. Thus, angular accelerations are different at these points. Hence, angular acceleration of the motion is not constant.

Notification Switch
Would you like to follow the 'Physics for k-12' conversation and receive update notifications?