| << Chapter < Page | Chapter >> Page > |
Tension in the rope must equal the weight of the supported mass, as we can prove by using Newton’s second law. If the 5.00 kg mass in the figure is stationary, then its acceleration is zero, so . The only external forces acting on the mass are its weight W and the tension T supplied by the rope. Summing the external forces to find the net force, we obtain
For a 5.00 kg mass (neglecting the mass of the rope), we see that
Another example of Newton’s third law in action is thrust. Rockets move forward by expelling gas backward at high velocity. This means that the rocket exerts a large force backward on the gas in the rocket combustion chamber, and the gas in turn exerts a large force forward on the rocket in response. This reaction force is called thrust.
The basics of problem solving, presented earlier in this text, are followed here with specific strategies for applying Newton’s laws of motion. These techniques also reinforce concepts that are useful in many other areas of physics.
First, identify the physical principles involved. If the problem involves forces, then Newton’s laws of motion are involved, and it is important to draw a careful sketch of the situation. Such a sketch is shown in [link] (a). Next, as in [link] (b), use vectors to represent all forces. Label the forces carefully and make sure that their lengths are proportional to the magnitude of the forces and that the arrows point in the direction in which the forces act.
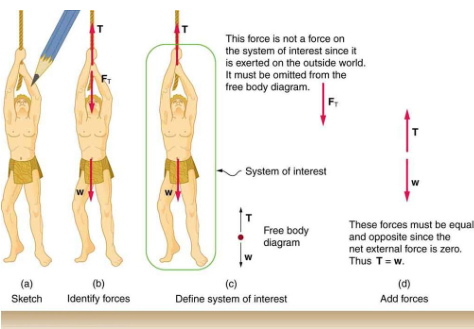
Next, make a list of “knowns and unknowns” and assign variable names to the quantities given in the problem. Figure out which variables need to be calculated; these are the “unknowns.” Now carefully define the system, meaning which objects are of interest for the problem. This decision is important, because Newton’s second law involves only external forces. Once the system is identified, it’s possible to see which forces are external and which are internal (see [link] (c)).
If the system acts on an object outside the system, you then know that the outside object exerts a force of equal magnitude but in the opposite direction on the system.
A diagram showing the system of interest and all the external forces acting on it is called a free-body diagram. Only external forces are shown on free-body diagrams, not acceleration or velocity. [link] (d) shows a free-body diagram for the system of interest.
After drawing a free-body diagram, apply Newton’s second law to solve the problem. This is done in [link] (d) for the case of Tarzan hanging from a vine. When external forces are clearly identified in the free-body diagram, translate the forces into equation form and solve for the unknowns. Note that forces acting in opposite directions have opposite signs. By convention, forces acting downward or to the left are usually negative.
| Unknowns | Knowns |
|
Force
a) Internal b) External c) Net |
Acceleration |
| Fnet = T-W-02 | Tension |
This video explains Newton’s third law of motion through examples involving push, normal force, and thrust (the force that propels a rocket or a jet). Think about this equation as you watch:
A physics teacher pushes a cart of demonstration equipment to a classroom, as in Image 4.12 Her mass is 65.0 kg, the cart’s mass is 12.0 kg, and the equipment’s mass is 7.0 kg. To push the cart forward, the teacher’s foot applies a force F foot of 150 N in the opposite direction (backward) on the floor. Calculate the acceleration produced by the teacher. The force of friction, which opposes the motion, is 24.0 N.

We should not include the forces F teacher , F cart , or F foot because these are exerted by the system, not on the system. We find the net external force by adding together the external forces acting on the system (see free-body diagram in the figure) and then use Newton’s second law to find the acceleration.
Newton’s second law is
The net external force on the system is the sum of the external forces: the force of the floor acting on the teacher, cart, and equipment (in the horizontal direction) and the force of friction. Because friction acts in the opposite direction, we assign it a negative value. Thus, for the net force, we obtain
The mass of the system is the sum of the mass of the teacher, cart, and equipment:
Insert these values of net F and m into Newton’s second law to obtain the acceleration of the system:
To investigate how mass affects tension in a connector, find a rubber band and some objects to hang from the end of the rubber band. How much does the rubber band stretch when a light object is hung from it?How much does it stretch when a heavier object is suspended? What does this show?Measure the mass of the object and the corresponding length of the rubber band in each case and plot a graph of mass vs length. (15 min) [link]

Notification Switch
Would you like to follow the 'Updated tutor hs physics content - legacy' conversation and receive update notifications?