| << Chapter < Page | Chapter >> Page > |
In this case, both final position vector and displacement are equal. This simplification, therefore, allows us to represent both displacement and position with a single vector variable r .
The three basic equations of motion with constant acceleration, as derived above, are :
These three equations completely describe motion of a point like mass, moving with constant acceleration. We need exactly five parameters to describe the motion under constant acceleration : .
It can be emphasized here that we can not use these equations if the acceleration is not constant. We should use basic differentiation or integration techniques for motion having variable acceleration (non-uniform acceleration). These equations serve to be a ready to use equations that avoids differentiation and integration. Further, it is evident that equations of motion are vector equations, involving vector addition. We can evaluate a motion under constant acceleration, using either graphical or algebraic method based on components.
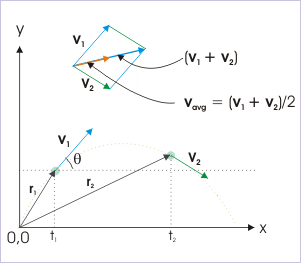
Here, we interpret these vector equations, using graphical technique. For illustration purpose, we apply these equations to a motion of an object, which is thrown at an angle θ from the horizontal. The magnitude of acceleration is "g", which is directed vertically downward. Let acceleration vector be represented by corresponding bold faced symbol g . Let and be the velocities at time instants and respectively and corresponding position vectors are and .
The final velocity at time instant , is given by :
Graphically, the final velocity is obtained by modifying initial vector by the vector .
Graphical representation of first equation

Now, we discuss graphical representation of second equation of motion. The average velocity between two time instants or two positions is given by :
The vector addition involved in the equation is graphically represented as shown in the figure. Note that average velocity is equal to half of the vector sum .
Graphical representation of second equation
Third equation of motion provides for displacement in terms of two vector quantities - initial velocity and acceleration. The displacement, s , is equal to addition of two vector terms :
Graphical representation of third equation

The application of equations of motion graphically is tedious. In general, we use component representation that allows us to apply equations algebraically. We use equations of motion, using component forms of vector quantities involved in the equations of motion. The component form of the various vector quantities are :
Using above relations, equations of motion are :
Problem : A particle is moving with an initial velocity , having an acceleration . Calculate its speed after 10 seconds.
Solution : The particle has acceleration of , which is a constant acceleration. Its magnitude is making an angle with x-direction. . Time interval is 10 seconds. Thus, applying equation of motion, we have :
Speed i.e. magnitude of velocity is :
We have discussed earlier that a vector quantity in one dimension can be conveniently expressed in terms of an equivalent system of scalar representation. The advantage of linear motion is that we can completely do away with vector notation with an appropriate scheme of assigning plus or minus signs to the quantities involved. The equivalent scalar representation takes advantage of the fact that vectors involved in linear motion has only two possible directions. The one in the direction of chosen axis is considered positive and the other against the direction of the chosen axis is considered negative.
At the same time, the concept of component allows us to treat a motion into an equivalent system of the three rectilinear motions in the mutually perpendicular directions along the axes. The two concepts, when combined together, renders it possible to treat equations of motion in scalar terms in mutually three perpendicular directions.
Once we follow the rules of equivalent scalar representation, we can treat equations of motion as scalar equations in the direction of an axis, say x - axis, as :
We have similar set of equations in the remaining two directions. We can obtain the composite interpretation of the motion by combing the individual result in each direction. In order to grasp the method, we rework the earlier example.
Problem : A particle is moving with an initial velocity , having an acceleration . Calculate its speed after 10 seconds.
Solution : The motion in x – direction :
The motion in y – direction :
Therefore, the velocity is :

Notification Switch
Would you like to follow the 'Physics for k-12' conversation and receive update notifications?