| << Chapter < Page | Chapter >> Page > |
The force constant is related to the rigidity (or stiffness) of a system—the larger the force constant, the greater the restoring force, and the stiffer the system. The units of are newtons per meter (N/m). For example, is directly related to Young’s modulus when we stretch a string. [link] shows a graph of the absolute value of the restoring force versus the displacement for a system that can be described by Hooke’s law—a simple spring in this case. The slope of the graph equals the force constant in newtons per meter. A common physics laboratory exercise is to measure restoring forces created by springs, determine if they follow Hooke’s law, and calculate their force constants if they do.
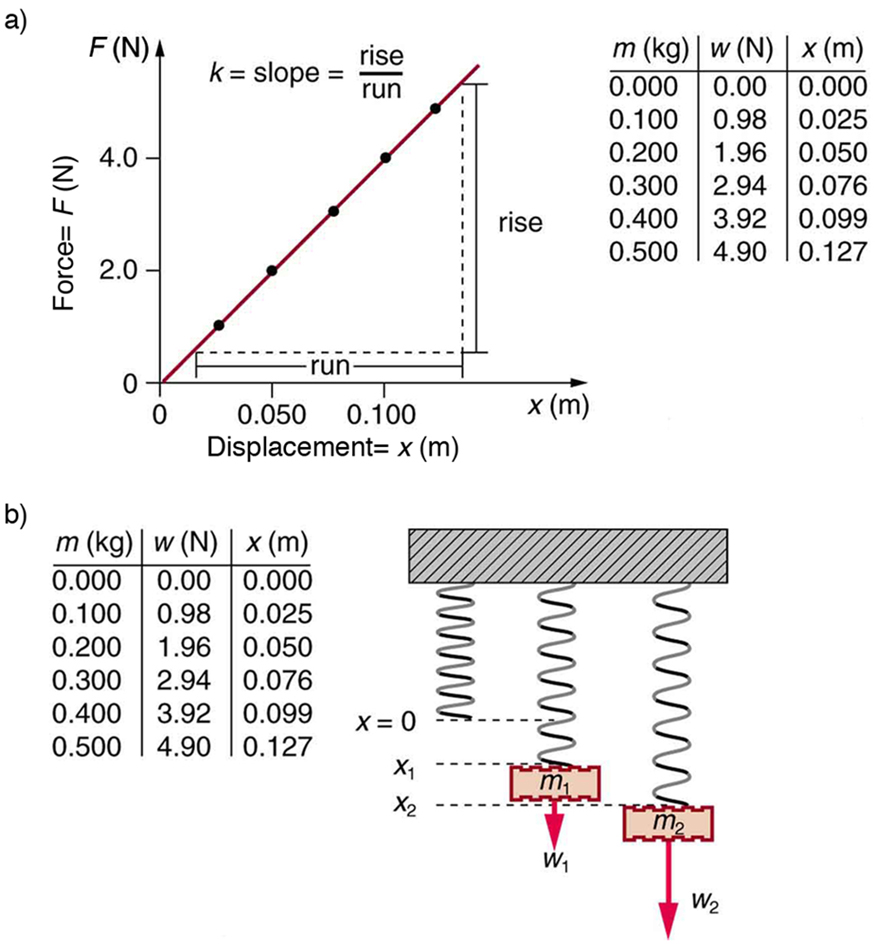

What is the force constant for the suspension system of a car that settles 1.20 cm when an 80.0-kg person gets in?
Strategy
Consider the car to be in its equilibrium position before the person gets in. The car then settles down 1.20 cm, which means it is displaced to a position . At that point, the springs supply a restoring force equal to the person’s weight . We take this force to be in Hooke’s law. Knowing and , we can then solve the force constant .
Solution
Substitute known values and solve :
Discussion
Note that and have opposite signs because they are in opposite directions—the restoring force is up, and the displacement is down. Also, note that the car would oscillate up and down when the person got in if it were not for damping (due to frictional forces) provided by shock absorbers. Bouncing cars are a sure sign of bad shock absorbers.
In order to produce a deformation, work must be done. That is, a force must be exerted through a distance, whether you pluck a guitar string or compress a car spring. If the only result is deformation, and no work goes into thermal, sound, or kinetic energy, then all the work is initially stored in the deformed object as some form of potential energy. The potential energy stored in a spring is . Here, we generalize the idea to elastic potential energy for a deformation of any system that can be described by Hooke’s law. Hence,
where is the elastic potential energy stored in any deformed system that obeys Hooke’s law and has a displacement from equilibrium and a force constant .

Notification Switch
Would you like to follow the 'College physics for ap® courses' conversation and receive update notifications?