| << Chapter < Page | Chapter >> Page > |
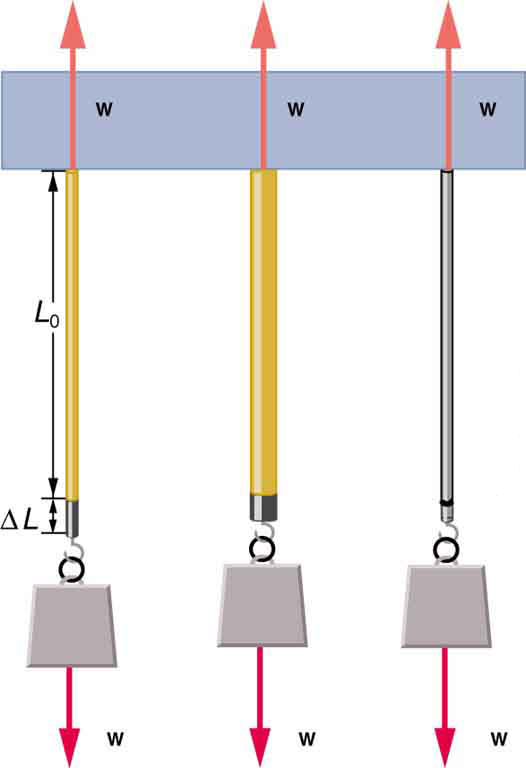
How would you go about measuring the proportionality constant of a rubber band? If a rubber band stretched 3 cm when a 100-g mass was attached to it, then how much would it stretch if two similar rubber bands were attached to the same mass—even if put together in parallel or alternatively if tied together in series?
We now consider three specific types of deformations: changes in length (tension and compression), sideways shear (stress), and changes in volume. All deformations are assumed to be small unless otherwise stated.
A change in length is produced when a force is applied to a wire or rod parallel to its length , either stretching it (a tension) or compressing it. (See [link] .)
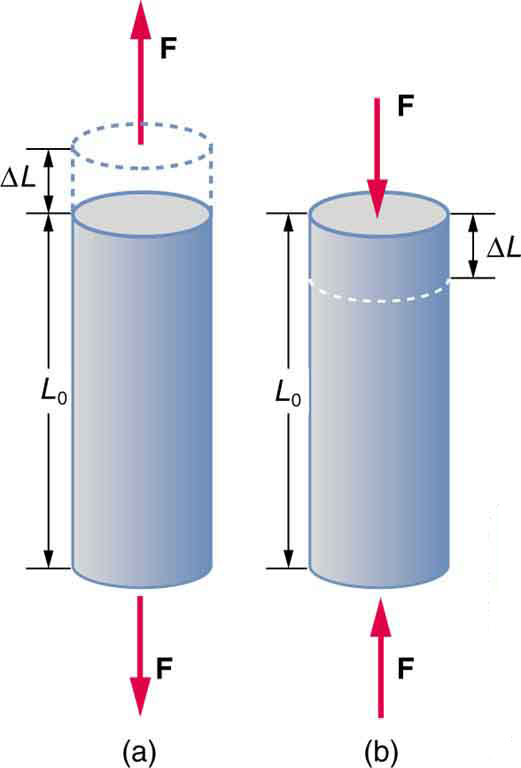
Experiments have shown that the change in length ( ) depends on only a few variables. As already noted, is proportional to the force and depends on the substance from which the object is made. Additionally, the change in length is proportional to the original length and inversely proportional to the cross-sectional area of the wire or rod. For example, a long guitar string will stretch more than a short one, and a thick string will stretch less than a thin one. We can combine all these factors into one equation for :
where is the change in length, the applied force, is a factor, called the elastic modulus or Young's modulus, that depends on the substance, is the cross-sectional area, and is the original length. [link] lists values of for several materials—those with a large are said to have a large tensile strength because they deform less for a given tension or compression.
| Material | Young's modulus (tension–compression) Y | Shear modulus S | Bulk modulus B |
|---|---|---|---|
| Aluminum | 70 | 25 | 75 |
| Bone – tension | 16 | 80 | 8 |
| Bone – compression | 9 | ||
| Brass | 90 | 35 | 75 |
| Brick | 15 | ||
| Concrete | 20 | ||
| Glass | 70 | 20 | 30 |
| Granite | 45 | 20 | 45 |
| Hair (human) | 10 | ||
| Hardwood | 15 | 10 | |
| Iron, cast | 100 | 40 | 90 |
| Lead | 16 | 5 | 50 |
| Marble | 60 | 20 | 70 |
| Nylon | 5 | ||
| Polystyrene | 3 | ||
| Silk | 6 | ||
| Spider thread | 3 | ||
| Steel | 210 | 80 | 130 |
| Tendon | 1 | ||
| Acetone | 0.7 | ||
| Ethanol | 0.9 | ||
| Glycerin | 4.5 | ||
| Mercury | 25 | ||
| Water | 2.2 |
Young's moduli are not listed for liquids and gases in [link] because they cannot be stretched or compressed in only one direction. Note that there is an assumption that the object does not accelerate, so that there are actually two applied forces of magnitude acting in opposite directions. For example, the strings in [link] are being pulled down by a force of magnitude and held up by the ceiling, which also exerts a force of magnitude .

Notification Switch
Would you like to follow the 'College physics for ap® courses' conversation and receive update notifications?