| << Chapter < Page | Chapter >> Page > |
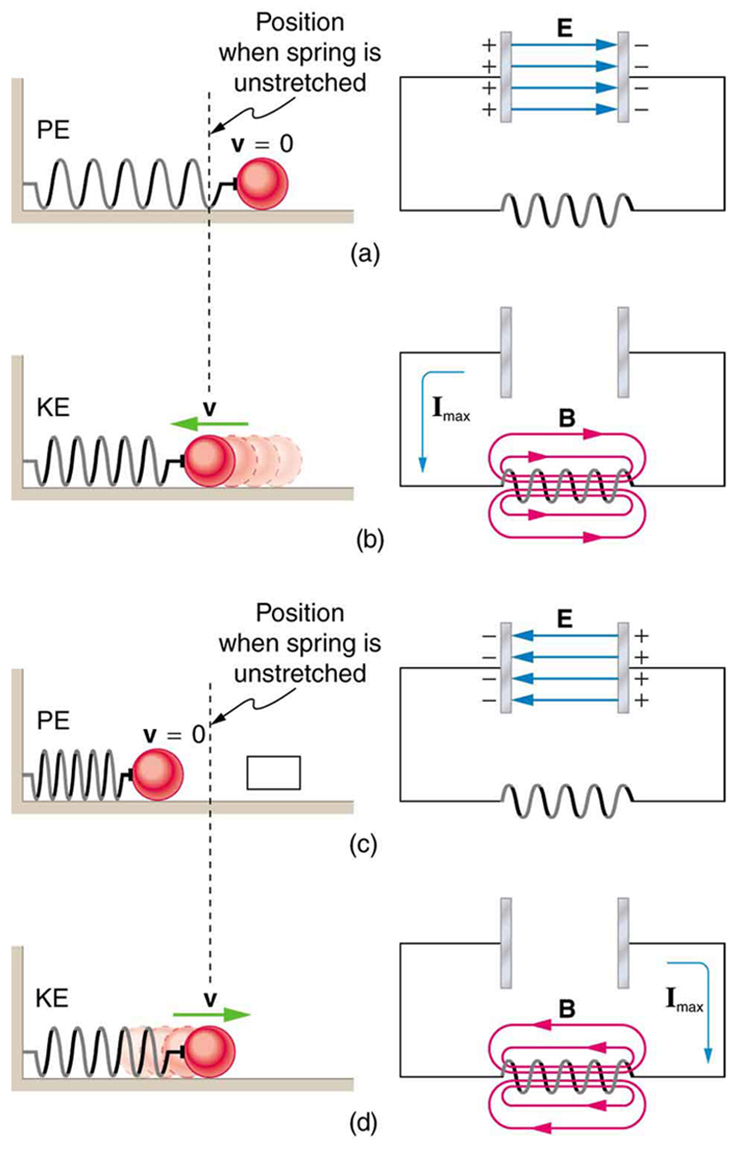
A pure LC circuit with negligible resistance oscillates at , the same resonant frequency as an RLC circuit. It can serve as a frequency standard or clock circuit—for example, in a digital wristwatch. With a very small resistance, only a very small energy input is necessary to maintain the oscillations. The circuit is analogous to a car with no shock absorbers. Once it starts oscillating, it continues at its natural frequency for some time. [link] shows the analogy between an LC circuit and a mass on a spring.
Build circuits with capacitors, inductors, resistors and AC or DC voltage sources, and inspect them using lab instruments such as voltmeters and ammeters.

Does the resonant frequency of an AC circuit depend on the peak voltage of the AC source? Explain why or why not.
Suppose you have a motor with a power factor significantly less than 1. Explain why it would be better to improve the power factor as a method of improving the motor’s output, rather than to increase the voltage input.
An RL circuit consists of a resistor and a 3.00 mH inductor. (a) Find its impedance at 60.0 Hz and 10.0 kHz. (b) Compare these values of with those found in [link] in which there was also a capacitor.
(a) at 60.0 Hz, at 10.0 kHz
(b) At 60 Hz, with a capacitor, , over 13 times as high as without the capacitor. The capacitor makes a large difference at low frequencies. At 10 kHz, with a capacitor , about the same as without the capacitor. The capacitor has a smaller effect at high frequencies.
An RC circuit consists of a resistor and a capacitor. (a) Find its impedance at 60.0 Hz and 10.0 kHz. (b) Compare these values of with those found in [link] , in which there was also an inductor.
An LC circuit consists of a inductor and a capacitor. (a) Find its impedance at 60.0 Hz and 10.0 kHz. (b) Compare these values of with those found in [link] in which there was also a resistor.
(a) at 60.0 Hz, at 10.0 kHz
(b) These values are close to those obtained in [link] because at low frequency the capacitor dominates and at high frequency the inductor dominates. So in both cases the resistor makes little contribution to the total impedance.
What is the resonant frequency of a 0.500 mH inductor connected to a capacitor?
To receive AM radio, you want an RLC circuit that can be made to resonate at any frequency between 500 and 1650 kHz. This is accomplished with a fixed inductor connected to a variable capacitor. What range of capacitance is needed?
9.30 nF to 101 nF
Suppose you have a supply of inductors ranging from 1.00 nH to 10.0 H, and capacitors ranging from 1.00 pF to 0.100 F. What is the range of resonant frequencies that can be achieved from combinations of a single inductor and a single capacitor?
What capacitance do you need to produce a resonant frequency of 1.00 GHz, when using an 8.00 nH inductor?
3.17 pF
What inductance do you need to produce a resonant frequency of 60.0 Hz, when using a capacitor?
The lowest frequency in the FM radio band is 88.0 MHz. (a) What inductance is needed to produce this resonant frequency if it is connected to a 2.50 pF capacitor? (b) The capacitor is variable, to allow the resonant frequency to be adjusted to as high as 108 MHz. What must the capacitance be at this frequency?
(a)
(b) 1.66 pF
An RLC series circuit has a resistor, a inductor, and an capacitor.(a) Find the circuit’s impedance at 120 Hz. (b) Find the circuit’s impedance at 5.00 kHz. (c) If the voltage source has , what is at each frequency? (d) What is the resonant frequency of the circuit? (e) What is at resonance?
An RLC series circuit has a resistor, a inductor, and a 25.0 nF capacitor. (a) Find the circuit’s impedance at 500 Hz. (b) Find the circuit’s impedance at 7.50 kHz. (c) If the voltage source has , what is at each frequency? (d) What is the resonant frequency of the circuit? (e) What is at resonance?
(a)
(b)
(c) 31.9 mA at 500 Hz, 312 mA at 7.50 kHz
(d) 82.2 kHz
(e) 0.408 A
An RLC series circuit has a resistor, a inductor, and an capacitor. (a) Find the power factor at . (b) What is the phase angle at 120 Hz? (c) What is the average power at 120 Hz? (d) Find the average power at the circuit’s resonant frequency.
An RLC series circuit has a resistor, a inductor, and a 25.0 nF capacitor. (a) Find the power factor at . (b) What is the phase angle at this frequency? (c) What is the average power at this frequency? (d) Find the average power at the circuit’s resonant frequency.
(a) 0.159
(b)
(c) 26.4 W
(d) 166 W
An RLC series circuit has a resistor and a 25.0 mH inductor. At 8000 Hz, the phase angle is . (a) What is the impedance? (b) Find the circuit’s capacitance. (c) If is applied, what is the average power supplied?
Referring to [link] , find the average power at 10.0 kHz.
16.0 W

Notification Switch
Would you like to follow the 'College physics ii' conversation and receive update notifications?