| << Chapter < Page | Chapter >> Page > |
Another example of thermal stress is found in the mouth. Dental fillings can expand differently from tooth enamel. It can give pain when eating ice cream or having a hot drink. Cracks might occur in the filling. Metal fillings (gold, silver, etc.) are being replaced by composite fillings (porcelain), which have smaller coefficients of expansion, and are closer to those of teeth.
Two blocks, A and B, are made of the same material. Block A has dimensions and Block B has dimensions . If the temperature changes, what is (a) the change in the volume of the two blocks, (b) the change in the cross-sectional area , and (c) the change in the height of the two blocks?
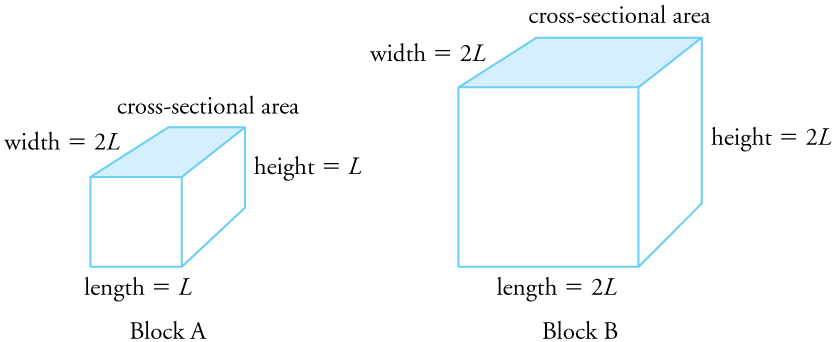
(a) The change in volume is proportional to the original volume. Block A has a volume of . Block B has a volume of which is 4 times that of Block A. Thus the change in volume of Block B should be 4 times the change in volume of Block A.
(b) The change in area is proportional to the area. The cross-sectional area of Block A is while that of Block B is Because cross-sectional area of Block B is twice that of Block A, the change in the cross-sectional area of Block B is twice that of Block A.
(c) The change in height is proportional to the original height. Because the original height of Block B is twice that of A, the change in the height of Block B is twice that of Block A.
Thermal stresses caused by uneven cooling can easily break glass cookware. Explain why Pyrex®, a glass with a small coefficient of linear expansion, is less susceptible.
Water expands significantly when it freezes: a volume increase of about 9% occurs. As a result of this expansion and because of the formation and growth of crystals as water freezes, anywhere from 10% to 30% of biological cells are burst when animal or plant material is frozen. Discuss the implications of this cell damage for the prospect of preserving human bodies by freezing so that they can be thawed at some future date when it is hoped that all diseases are curable.
One method of getting a tight fit, say of a metal peg in a hole in a metal block, is to manufacture the peg slightly larger than the hole. The peg is then inserted when at a different temperature than the block. Should the block be hotter or colder than the peg during insertion? Explain your answer.

Notification Switch
Would you like to follow the 'College physics for ap® courses' conversation and receive update notifications?