1. Home
  2. College physics
  3. Atomic physics
  4. Bohr’s theory of the hydrogen

30.3 Bohr’s theory of the hydrogen atom  (Page 2/14)

<< Chapter < Page
  College physics     Page 2 / 14
Chapter >> Page >

The observed hydrogen-spectrum wavelengths can be calculated using the following formula:

1 λ = R 1 n f 2 − 1 n i 2 , size 12{ { {1} over {λ} } =R left ( { {1} over {n rSub { size 8{f} } rSup { size 8{2} } } } - { {1} over {n rSub { size 8{i} } rSup { size 8{2} } } } right )} {}

where λ size 12{λ} {} is the wavelength of the emitted EM radiation and R size 12{R} {} is the Rydberg constant    , determined by the experiment to be

R = 1 . 097 × 10 7 / m ( or m − 1 ) . size 12{R=1 "." "097" times "10" rSup { size 8{7} } `/"m " \( "or m" rSup { size 8{ - 1} } \) } {}

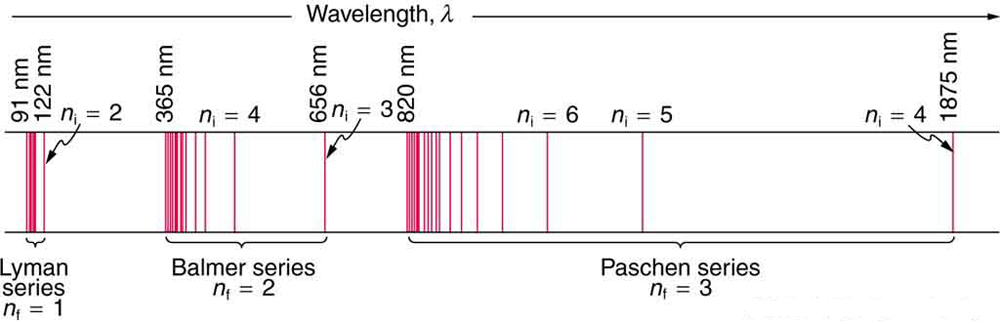
The constant n f is a positive integer associated with a specific series. For the Lyman series, n f = 1 ; for the Balmer series, n f = 2 ; for the Paschen series, n f = 3 ; and so on. The Lyman series is entirely in the UV, while part of the Balmer series is visible with the remainder UV. The Paschen series and all the rest are entirely IR. There are apparently an unlimited number of series, although they lie progressively farther into the infrared and become difficult to observe as n f increases. The constant n i is a positive integer, but it must be greater than n f . Thus, for the Balmer series, n f = 2 and n i = 3, 4, 5, 6, ... . Note that n i size 12{n rSub { size 8{i} } } {} can approach infinity. While the formula in the wavelengths equation was just a recipe designed to fit data and was not based on physical principles, it did imply a deeper meaning. Balmer first devised the formula for his series alone, and it was later found to describe all the other series by using different values of n f size 12{n rSub { size 8{f} } } {} . Bohr was the first to comprehend the deeper meaning. Again, we see the interplay between experiment and theory in physics. Experimentally, the spectra were well established, an equation was found to fit the experimental data, but the theoretical foundation was missing.

The figure shows three horizontal lines at small distances from each other. Between the two lower lines, the Lyman series, with four vertical red bands in compact form, is shown. The value of the constant n sub f is 1 and the wavelengths are ninety-one nanometers to one hundred nanometers. The Balmer series is shown to the right side of this series. The value of the constant n sub f is two, and the range of wavelengths is from three hundred sixty five to six hundred fifty six nanometers. At the right side of this, the Paschen series bands are shown. The value of the constant n sub f is three, and the range of the wavelengths is from eight hundred twenty nanometers to one thousand eight hundred and seventy five nanometers.
A schematic of the hydrogen spectrum shows several series named for those who contributed most to their determination. Part of the Balmer series is in the visible spectrum, while the Lyman series is entirely in the UV, and the Paschen series and others are in the IR. Values of n f size 12{n rSub { size 8{f} } } {} and n i size 12{n rSub { size 8{f} } } {} are shown for some of the lines.

Calculating wave interference of a hydrogen line

What is the distance between the slits of a grating that produces a first-order maximum for the second Balmer line at an angle of 15º size 12{"15"°} {} ?

Strategy and Concept

For an Integrated Concept problem, we must first identify the physical principles involved. In this example, we need to know (a) the wavelength of light as well as (b) conditions for an interference maximum for the pattern from a double slit. Part (a) deals with a topic of the present chapter, while part (b) considers the wave interference material of Wave Optics .

Solution for (a)

Hydrogen spectrum wavelength . The Balmer series requires that n f = 2 size 12{n rSub { size 8{f} } =2} {} . The first line in the series is taken to be for n i = 3 size 12{n rSub { size 8{i} } =3} {} , and so the second would have n i = 4 size 12{n rSub { size 8{i} } =4} {} .

The calculation is a straightforward application of the wavelength equation. Entering the determined values for n f size 12{n rSub { size 8{f} } } {} and n i size 12{n rSub { size 8{i} } } {} yields

1 λ = R 1 n f 2 − 1 n i 2 = 1.097 × 10 7 m –1 1 2 2 − 1 4 2 = 2.057 × 10 6 m –1 .

Inverting to find λ size 12{λ} {} gives

λ = 1 2.057 × 10 6 m –1 = 486 × 10 − 9 m = 486 nm. alignl { stack { size 12{λ= { {1} over {2 "." "057" times "10" rSup { size 8{6} } " /m"} } ="486" times "10" rSup { size 8{ - 9} } " m"} {} #="486"`"nm" "." {} } } {}

Discussion for (a)

This is indeed the experimentally observed wavelength, corresponding to the second (blue-green) line in the Balmer series. More impressive is the fact that the same simple recipe predicts all of the hydrogen spectrum lines, including new ones observed in subsequent experiments. What is nature telling us?

Solution for (b)

Double-slit interference ( Wave Optics ). To obtain constructive interference for a double slit, the path length difference from two slits must be an integral multiple of the wavelength. This condition was expressed by the equation

d sin θ = mλ , size 12{d"sin"θ=mλ} {}

where d size 12{d} {} is the distance between slits and θ size 12{θ} {} is the angle from the original direction of the beam. The number m size 12{m} {} is the order of the interference; m = 1 size 12{m=1} {} in this example. Solving for d size 12{d} {} and entering known values yields

d = 1 486 nm sin 15º = 1.88 × 10 − 6 m . size 12{d= { { left (1 right ) left ("486"" nm" right )} over {"sin""15"°} } =1 "." "88" times "10" rSup { size 8{ - 6} } " m"} {}

Discussion for (b)

This number is similar to those used in the interference examples of Introduction to Quantum Physics (and is close to the spacing between slits in commonly used diffraction glasses).

Got questions? Get instant answers now!

Questions & Answers

what is biology
Hajah Reply
the study of living organisms and their interactions with one another and their environments
AI-Robot
what is biology
Victoria Reply
HOW CAN MAN ORGAN FUNCTION
Alfred Reply
the diagram of the digestive system
Assiatu Reply
allimentary cannel
Ogenrwot
How does twins formed
William Reply
They formed in two ways first when one sperm and one egg are splited by mitosis or two sperm and two eggs join together
Oluwatobi
what is genetics
Josephine Reply
Genetics is the study of heredity
Misack
how does twins formed?
Misack
What is manual
Hassan Reply
discuss biological phenomenon and provide pieces of evidence to show that it was responsible for the formation of eukaryotic organelles
Joseph Reply
what is biology
Yousuf Reply
the study of living organisms and their interactions with one another and their environment.
Wine
discuss the biological phenomenon and provide pieces of evidence to show that it was responsible for the formation of eukaryotic organelles in an essay form
Joseph Reply
what is the blood cells
Shaker Reply
list any five characteristics of the blood cells
Shaker
lack electricity and its more savely than electronic microscope because its naturally by using of light
Abdullahi Reply
advantage of electronic microscope is easily and clearly while disadvantage is dangerous because its electronic. advantage of light microscope is savely and naturally by sun while disadvantage is not easily,means its not sharp and not clear
Abdullahi
cell theory state that every organisms composed of one or more cell,cell is the basic unit of life
Abdullahi
is like gone fail us
DENG
cells is the basic structure and functions of all living things
Ramadan
What is classification
ISCONT Reply
is organisms that are similar into groups called tara
Yamosa
in what situation (s) would be the use of a scanning electron microscope be ideal and why?
Kenna Reply
A scanning electron microscope (SEM) is ideal for situations requiring high-resolution imaging of surfaces. It is commonly used in materials science, biology, and geology to examine the topography and composition of samples at a nanoscale level. SEM is particularly useful for studying fine details,
Hilary
cell is the building block of life.
Condoleezza Reply
Got questions? Join the online conversation and get instant answers!
Jobilize.com Reply
<< Chapter < Page Page > Chapter >>
Practice Key Terms 7

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, College physics. OpenStax CNX. Jul 27, 2015 Download for free at http://legacy.cnx.org/content/col11406/1.9
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'College physics' conversation and receive update notifications?

Ask