| << Chapter < Page | Chapter >> Page > |
[link] (a) shows a parallel connection of three capacitors with a voltage applied. Here the total capacitance is easier to find than in the series case. To find the equivalent total capacitance , we first note that the voltage across each capacitor is , the same as that of the source, since they are connected directly to it through a conductor. (Conductors are equipotentials, and so the voltage across the capacitors is the same as that across the voltage source.) Thus the capacitors have the same charges on them as they would have if connected individually to the voltage source. The total charge is the sum of the individual charges:
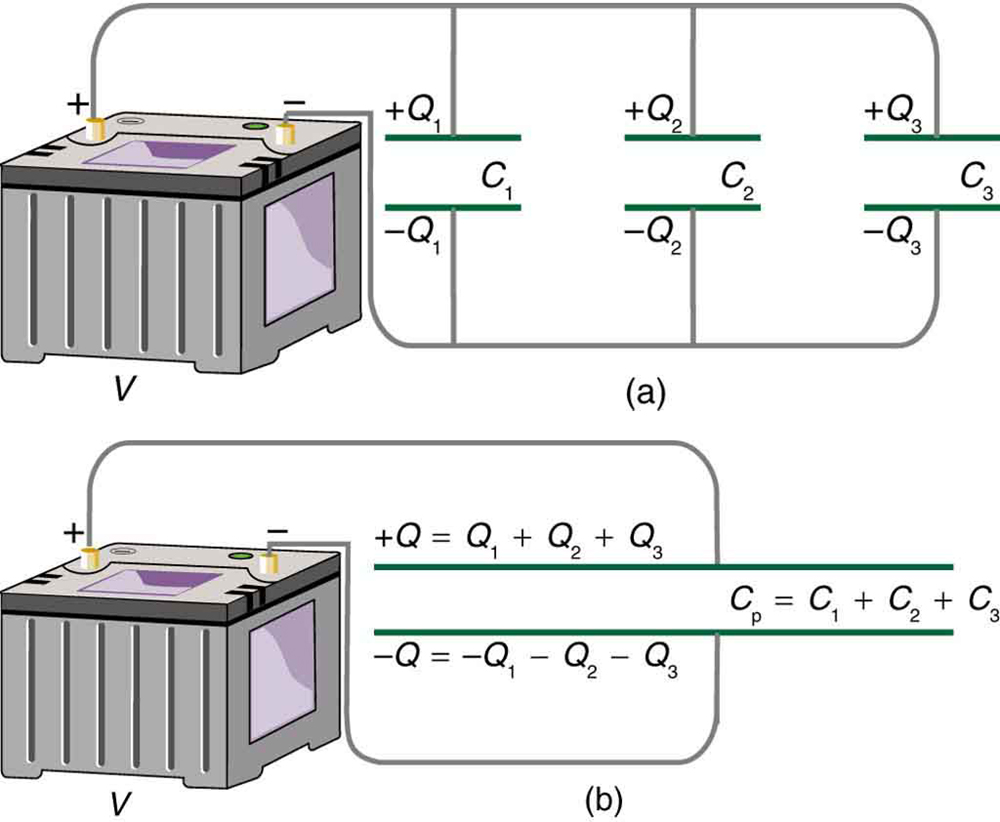
Using the relationship , we see that the total charge is , and the individual charges are , , and . Entering these into the previous equation gives
Canceling from the equation, we obtain the equation for the total capacitance in parallel :
Total capacitance in parallel is simply the sum of the individual capacitances. (Again the “ ... ” indicates the expression is valid for any number of capacitors connected in parallel.) So, for example, if the capacitors in the example above were connected in parallel, their capacitance would be
The equivalent capacitor for a parallel connection has an effectively larger plate area and, thus, a larger capacitance, as illustrated in [link] (b).
Total capacitance in parallel
More complicated connections of capacitors can sometimes be combinations of series and parallel. (See [link] .) To find the total capacitance of such combinations, we identify series and parallel parts, compute their capacitances, and then find the total.
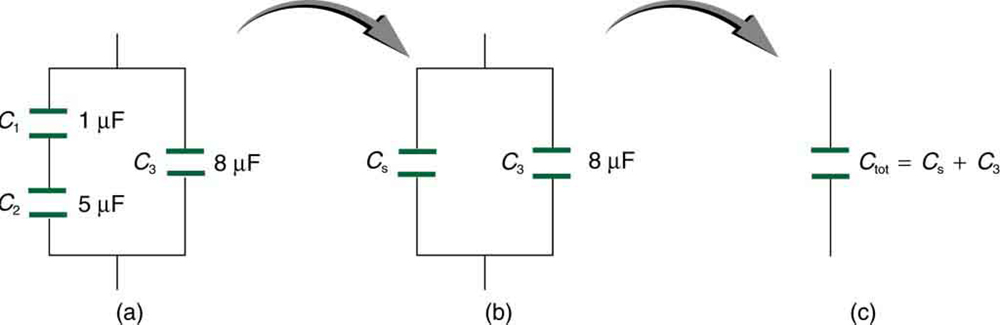
Find the total capacitance of the combination of capacitors shown in [link] . Assume the capacitances in [link] are known to three decimal places ( , , and ), and round your answer to three decimal places.
Strategy
To find the total capacitance, we first identify which capacitors are in series and which are in parallel. Capacitors and are in series. Their combination, labeled in the figure, is in parallel with .
Solution
Since and are in series, their total capacitance is given by . Entering their values into the equation gives
Inverting gives
This equivalent series capacitance is in parallel with the third capacitor; thus, the total is the sum
Discussion
This technique of analyzing the combinations of capacitors piece by piece until a total is obtained can be applied to larger combinations of capacitors.
If you wish to store a large amount of energy in a capacitor bank, would you connect capacitors in series or parallel? Explain.
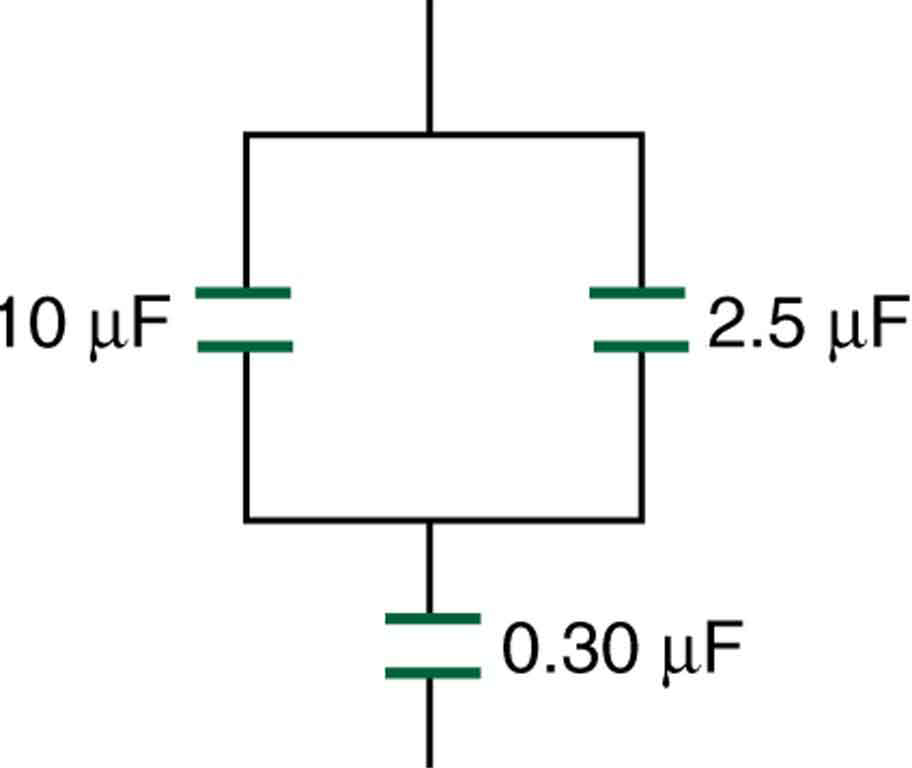
Find the total capacitance of the combination of capacitors in [link] .
Suppose you want a capacitor bank with a total capacitance of 0.750 F and you possess numerous 1.50 mF capacitors. What is the smallest number you could hook together to achieve your goal, and how would you connect them?
What total capacitances can you make by connecting a and an capacitor together?
in series combination, in parallel combination
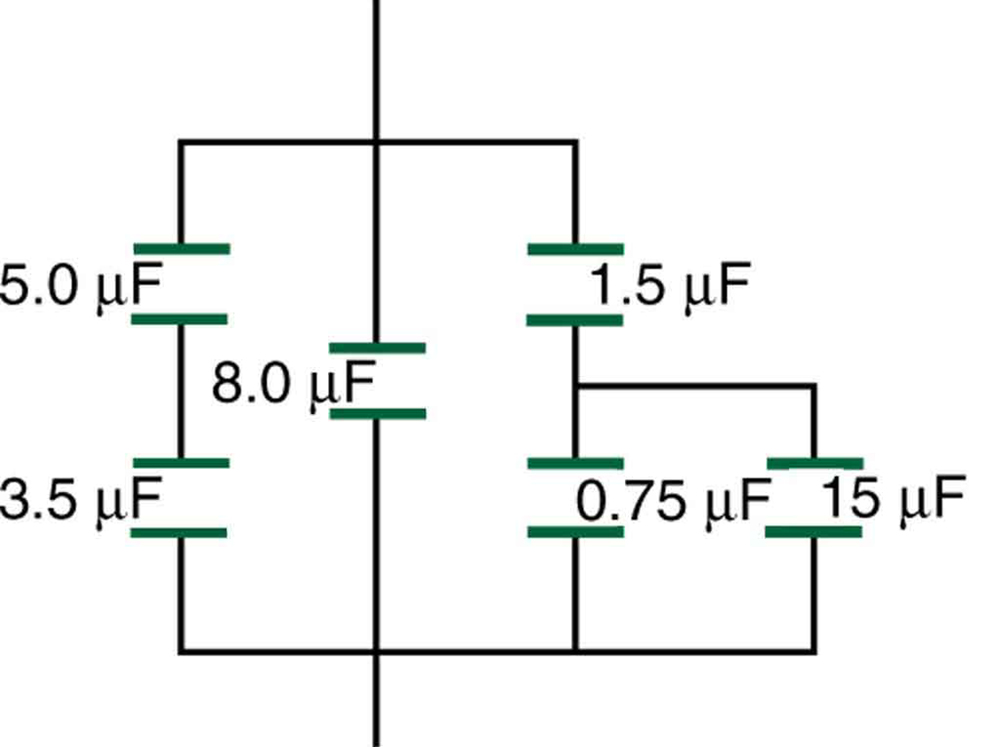
Find the total capacitance of the combination of capacitors shown in [link] .

Find the total capacitance of the combination of capacitors shown in [link] .
Unreasonable Results
(a) An capacitor is connected in parallel to another capacitor, producing a total capacitance of . What is the capacitance of the second capacitor? (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?
(a)
(b) You cannot have a negative value of capacitance.
(c) The assumption that the capacitors were hooked up in parallel, rather than in series, was incorrect. A parallel connection always produces a greater capacitance, while here a smaller capacitance was assumed. This could happen only if the capacitors are connected in series.

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?