| << Chapter < Page | Chapter >> Page > |
Point charges, such as electrons, are among the fundamental building blocks of matter. Furthermore, spherical charge distributions (like on a metal sphere) create external electric fields exactly like a point charge. The electric potential due to a point charge is, thus, a case we need to consider. Using calculus to find the work needed to move a test charge from a large distance away to a distance of from a point charge , and noting the connection between work and potential , it can be shown that the electric potential of a point charge is
where k is a constant equal to .
The electric potential of a point charge is given by
The potential at infinity is chosen to be zero. Thus for a point charge decreases with distance, whereas for a point charge decreases with distance squared:
Recall that the electric potential is a scalar and has no direction, whereas the electric field is a vector. To find the voltage due to a combination of point charges, you add the individual voltages as numbers. To find the total electric field, you must add the individual fields as vectors , taking magnitude and direction into account. This is consistent with the fact that is closely associated with energy, a scalar, whereas is closely associated with force, a vector.
Charges in static electricity are typically in the nanocoulomb to microcoulomb range. What is the voltage 5.00 cm away from the center of a 1-cm diameter metal sphere that has a static charge?
Strategy
As we have discussed in Electric Charge and Electric Field , charge on a metal sphere spreads out uniformly and produces a field like that of a point charge located at its center. Thus we can find the voltage using the equation .
Solution
Entering known values into the expression for the potential of a point charge, we obtain
Discussion
The negative value for voltage means a positive charge would be attracted from a larger distance, since the potential is lower (more negative) than at larger distances. Conversely, a negative charge would be repelled, as expected.
A demonstration Van de Graaff generator has a 25.0 cm diameter metal sphere that produces a voltage of 100 kV near its surface. (See [link] .) What excess charge resides on the sphere? (Assume that each numerical value here is shown with three significant figures.)
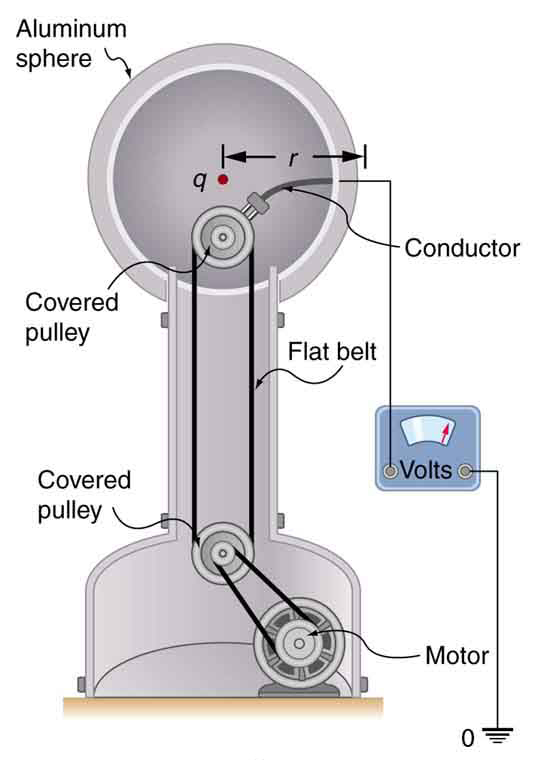
Strategy
The potential on the surface will be the same as that of a point charge at the center of the sphere, 12.5 cm away. (The radius of the sphere is 12.5 cm.) We can thus determine the excess charge using the equation
Solution
Solving for and entering known values gives
Discussion
This is a relatively small charge, but it produces a rather large voltage. We have another indication here that it is difficult to store isolated charges.

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?