| << Chapter < Page | Chapter >> Page > |
In the previous section, we explored the relationship between voltage and energy. In this section, we will explore the relationship between voltage and electric field. For example, a uniform electric field is produced by placing a potential difference (or voltage) across two parallel metal plates, labeled A and B. (See [link] .) Examining this will tell us what voltage is needed to produce a certain electric field strength; it will also reveal a more fundamental relationship between electric potential and electric field. From a physicist’s point of view, either or can be used to describe any charge distribution. is most closely tied to energy, whereas is most closely related to force. is a scalar quantity and has no direction, while is a vector quantity, having both magnitude and direction. (Note that the magnitude of the electric field strength, a scalar quantity, is represented by below.) The relationship between and is revealed by calculating the work done by the force in moving a charge from point A to point B. But, as noted in Electric Potential Energy: Potential Difference , this is complex for arbitrary charge distributions, requiring calculus. We therefore look at a uniform electric field as an interesting special case.
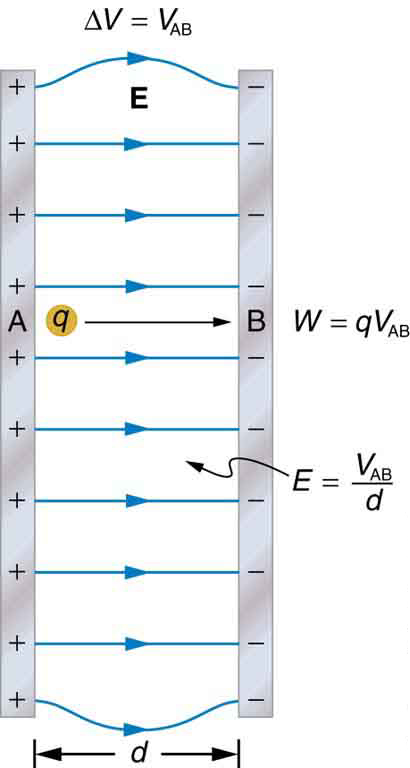
The work done by the electric field in [link] to move a positive charge from A, the positive plate, higher potential, to B, the negative plate, lower potential, is
The potential difference between points A and B is
Entering this into the expression for work yields
Work is ; here , since the path is parallel to the field, and so . Since , we see that . Substituting this expression for work into the previous equation gives
The charge cancels, and so the voltage between points A and B is seen to be
where is the distance from A to B, or the distance between the plates in [link] . Note that the above equation implies the units for electric field are volts per meter. We already know the units for electric field are newtons per coulomb; thus the following relation among units is valid:
where is the distance from A to B, or the distance between the plates.
Dry air will support a maximum electric field strength of about . Above that value, the field creates enough ionization in the air to make the air a conductor. This allows a discharge or spark that reduces the field. What, then, is the maximum voltage between two parallel conducting plates separated by 2.5 cm of dry air?
Strategy
We are given the maximum electric field between the plates and the distance between them. The equation can thus be used to calculate the maximum voltage.
Solution
The potential difference or voltage between the plates is
Entering the given values for and gives
or
(The answer is quoted to only two digits, since the maximum field strength is approximate.)
Discussion
One of the implications of this result is that it takes about 75 kV to make a spark jump across a 2.5 cm (1 in.) gap, or 150 kV for a 5 cm spark. This limits the voltages that can exist between conductors, perhaps on a power transmission line. A smaller voltage will cause a spark if there are points on the surface, since points create greater fields than smooth surfaces. Humid air breaks down at a lower field strength, meaning that a smaller voltage will make a spark jump through humid air. The largest voltages can be built up, say with static electricity, on dry days.

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?