This module is from Fundamentals of Mathematics by Denny Burzynski and Wade Ellis, Jr. This module discusses how to solve equations of the form
and
. By the end of the module students should understand the meaning and function of an equation, understand what is meant by the solution to an equation and be able to solve equations of the form
and
.
Section overview
- Equations
- Solutions and Equivalent Equations
- Solving Equations
Equations
Equation
An equation is a statement that two algebraic expressions are equal.
The following are examples of equations:
Notice that
,
, and
are
not equations. They are expressions. They are not equations because there is no statement that each of these expressions is equal to another expression.
Solutions and equivalent equations
Conditional equations
The truth of some equations is conditional upon the value chosen for the variable. Such equations are called
conditional equations . There are two additional types of equations. They are examined in courses in algebra, so we will not consider them now.
Solutions and solving an equation
The set of values that, when substituted for the variables, make the equation true, are called the
solutions of the equation.
An equation has been
solved when all its solutions have been found.
Sample set a
Verify that 3 is a solution to
.
When
,
Verify that
is a solution to
When
,
Verify that 5 is not a solution to
.
When
,
Verify that -2 is a solution to
.
When
,
Practice set a
Verify that 5 is a solution to
.
Substitute 5 into
.
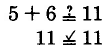 Thus, 5 is a solution.
Thus, 5 is a solution.
Verify that
is a solution to
.
Substitute -5 into
.
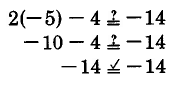 Thus, -5 is a solution.
Thus, -5 is a solution.
Verify that 0 is a solution to
.
Substitute 0 into
.
 Thus, 0 is a solution.
Thus, 0 is a solution.
Verify that 3 is not a solution to
.
Substitute 3 into
.
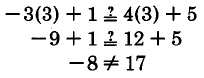 Thus, 3 is not a solution.
Thus, 3 is not a solution.
Verify that -1 is a solution to
.
Substitute -1 into
.
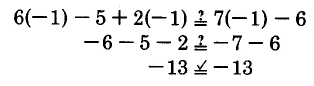 Thus, -1 is a solution.
Thus, -1 is a solution.
Equivalent equations
Some equations have precisely the same collection of solutions. Such equations are called equivalent equations. For example,
,
, and
are all equivalent equations since the only solution to each is
. (Can you verify this?)
Solving equations
We know that the equal sign of an equation indicates that the number represented by the expression on the left side is the same as the number represented by the expression on the right side.
| This number |
is the same as |
this number |
| ↓ |
↓ |
↓ |
|
|
= |
4 |
|
|
= |
11 |
|
|
= |
-1 |
![]() Thus, 5 is a solution.
Thus, 5 is a solution.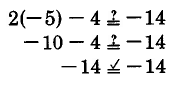 Thus, -5 is a solution.
Thus, -5 is a solution. Thus, 0 is a solution.
Thus, 0 is a solution.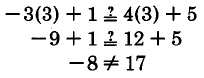 Thus, 3 is not a solution.
Thus, 3 is not a solution.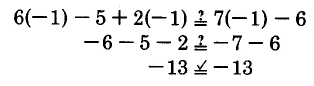 Thus, -1 is a solution.
Thus, -1 is a solution.