| << Chapter < Page | Chapter >> Page > |
Identifiseer die veranderlikes en die konstantes in die volgende vergelykings:
In die verlede het jy gesien veranderlikes kan relasies (verhoudings) hê met mekaar. Byvoorbeeld, Anton is 2 jaar ouer as Naomi. Die relasie of verband tussen die ouderdomme van Anton en Naomi kan geskryf word as , waar Anton se ouderdom voorgestel word met en Naomi se ouderdom voorgestel word met .
In die algemeen is 'n relasie 'n vergelyking met twee veranderlikes. Byvoorbeeld, en is relasies. In albei voorbeelde is en veranderlikes en 5 is 'n konstante. Vir elke waarde van sal jy 'n ander, unieke waarde vir kry.
Mens hoef nie relasies as vergelykings te skryf nie, dit kan ook weergegee word in woorde, tabelle of grafieke. Byvoorbeeld, in plaas van te skryf, kan mens sê “ is vyf keer so groot as ”. Ons kan ook die volgende tabel gee:
| 2 | 10 |
| 6 | 30 |
| 8 | 40 |
| 13 | 65 |
| 15 | 75 |
Voltooi die volgende tabel vir die gegewe funksies:
| 1 | |||
| 2 | |||
| 3 | |||
| 50 | |||
| 100 |
Wanneer ons met funksies met reële getalle werk, is ons vernaamste stuk gereedskap 'n grafiek. Eerstens, indien ons twee reële veranderlikes het, en , kan ons gelyktydig vir hulle waardes toeken. Byvoorbeeld, ons kan sê " is 5 en is 3”. Net soos wat ons vir " is 5” verkort deur te skryf " ”, kan ons ook “ is 5 en is 3” verkort deur te sê “ ”. Gewoonlik as ons dink aan reële getalle, dink ons aan 'n oneindige lang lyn en 'n getal as 'n punt op die lyn. Indien ons twee getalle op dieselfde tyd kies, kan ons iets soortgelyks doen, maar nou gebruik ons twee dimensies. Ons gebruik nou twee lyne, een vir en een vir , met die lyn vir , geroteer, soos in [link] .Ons noem dit die Cartesiese vlak .
Om 'n grafiek van 'n funksie te teken, moet ons 'n paar punte bereken en stip op die Cartesiese vlak. Die punte word dan in volgorde verbind om 'n gladde lyn te vorm.
Kom ons kyk na die funksie, . Ons kan dan al die punte beskou wat so is dat , in hierdie geval . Byvoorbeeld en stel sulke punte voor en stel nie so 'n punt voor nie, aangesien . Indien ons 'n kol op al die punte sit, asook al die soortgelyke punte vir alle moontlike waardes van , sal ons die grafiek soos in [link] kry.
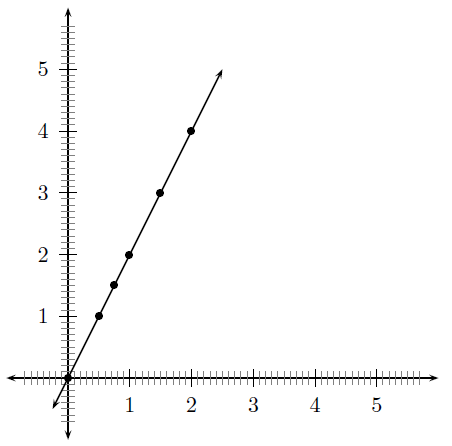
Die vorm van die grafiek is baie eenvoudig, dit is bloot ’n reguitlyn deur die middel van die vlak. Hierdie "stippingstegniek" is die sleutel tot die verstaan van funksies.
Stip die volgende punte en trek 'n gladde lyn deur hulle: (-6; -8), (-2; 0), (2; 8), (6; 16).
Tot dus ver het ons gesien jy kan
gebruik om 'n funksie voor te stel. Hierdie notasie raak verwarrend as jy met meer as een funksie werk. 'n Meer algemene manier om funksies neer te skryf, is deur die notasie
, te gebruik, waar

Notification Switch
Would you like to follow the 'Siyavula textbooks: wiskunde (graad 10) [caps]' conversation and receive update notifications?