| << Chapter < Page | Chapter >> Page > |
We will often use this notation when we solve similar triangles because it will help us match up the corresponding side lengths.
and are similar triangles. The lengths of two sides of each triangle are shown. Find the lengths of the third side of each triangle.
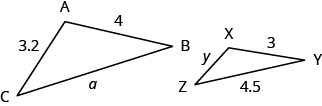
| Step 1. Read the problem. Draw the figure and label it with the given information. | The figure is provided. |
| Step 2. Identify what you are looking for. | The length of the sides of similar triangles |
| Step 3. Name. Choose a variable to represent it. | Let
a = length of the third side of y = length of the third side |
| Step 4. Translate. | |
| The triangles are similar, so the corresponding sides are in the same ratio. So
Since the side corresponds to the side , we will use the ratio to find the other sides. Be careful to match up corresponding sides correctly. 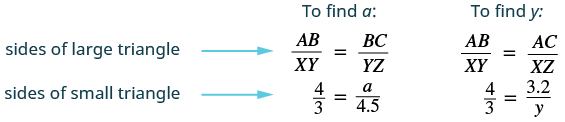 | |
| Step 5. Solve the equation. |
 |
Step 6.
Check:
 |
|
| Step 7. Answer the question. | The third side of is 6 and the third side of is 2.4. |
The Pythagorean Theorem is a special property of right triangles that has been used since ancient times. It is named after the Greek philosopher and mathematician Pythagoras who lived around BCE.
Remember that a right triangle has a angle, which we usually mark with a small square in the corner. The side of the triangle opposite the angle is called the hypotenuse , and the other two sides are called the legs . See [link] .
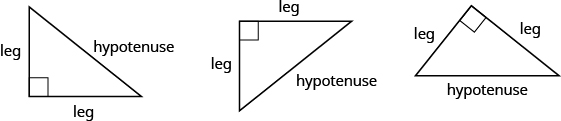
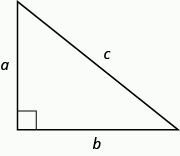
The Pythagorean Theorem tells how the lengths of the three sides of a right triangle relate to each other. It states that in any right triangle, the sum of the squares of the two legs equals the square of the hypotenuse.
In any right triangle
where is the length of the hypotenuse and are the lengths of the legs.
To solve problems that use the Pythagorean Theorem, we will need to find square roots. In Simplify and Use Square Roots we introduced the notation and defined it in this way:
For example, we found that is because
We will use this definition of square roots to solve for the length of a side in a right triangle.
Use the Pythagorean Theorem to find the length of the hypotenuse.
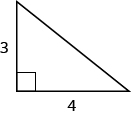
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | the length of the hypotenuse of the triangle |
| Step 3. Name. Choose a variable to represent it. | Let
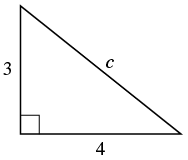 |
| Step 4.
Translate.
Write the appropriate formula. Substitute. |
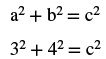 |
| Step 5. Solve the equation. |
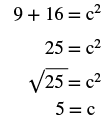 |
Step 6.
Check:
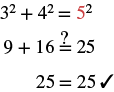 |
|
| Step 7. Answer the question. | The length of the hypotenuse is 5. |
Use the Pythagorean Theorem to find the length of the hypotenuse.
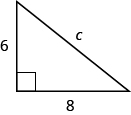
10
Use the Pythagorean Theorem to find the length of the hypotenuse.
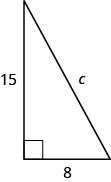
17
Use the Pythagorean Theorem to find the length of the longer leg.
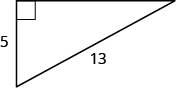
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | The length of the leg of the triangle |
| Step 3. Name. Choose a variable to represent it. | Let
Label side b 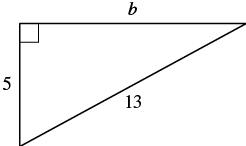 |
| Step 4.
Translate.
Write the appropriate formula. Substitute. |
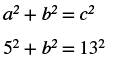 |
| Step 5.
Solve the equation. Isolate the variable term. Use the definition of the square root.
Simplify. |
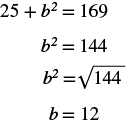 |
Step 6.
Check:
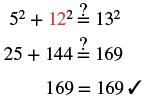 |
|
| Step 7. Answer the question. | The length of the leg is 12. |

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?