| << Chapter < Page | Chapter >> Page > |
Velocity is the rate of change of displacement.
Instantaneous velocity is the velocity of a body at a specific instant in time.
Average velocity is the total displacement of a body over a time interval.
Velocity is the rate of change of position. It tells us how much an object's position changes in time. This is the same as the displacement divided by the time taken. Since displacement is a vector and time taken is a scalar, velocity is also a vector. We use the symbol for velocity. If we have a displacement of and a time taken of , is then defined as:
Velocity can be positive or negative. Positive values of velocity mean that the object is moving away from the reference point or origin and negative values mean that the object is moving towards the reference point or origin.
Average velocity (symbol ) is the displacement for the whole motion divided by the time taken for the whole motion. Instantaneous velocity is the velocity at a specific instant in time.
(Average) Speed (symbol ) is the distance travelled ( ) divided by the time taken ( ) for the journey. Distance and time are scalars and therefore speed will also be a scalar. Speed is calculated as follows:
Instantaneous speed is the magnitude of instantaneous velocity. It has the same value, but no direction.
James walks 2 km away from home in 30 minutes. He then turns around and walks back home along the same path, also in 30 minutes. Calculate James' average speed and average velocity.

The question explicitly gives
The information is not in SI units and must therefore be converted.
To convert km to m, we know that:
Similarly, to convert 30 minutes to seconds,
James started at home and returned home, so his displacement is 0 m.
James walked a total distance of 4 000 m (2 000 m out and 2 000 m back).
James took 1 800 s to walk out and 1 800 s to walk back.
A man runs around a circular track of radius . It takes him to complete a revolution of the track. If he runs at constant speed, calculate:
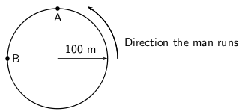
To determine the man's speed we need to know the distance he travels and how long it takes. We know it takes 120 s to complete one revolution ofthe track.(A revolution is to go around the track once.)
What distance is one revolution of the track? We know the track is a circle and we know its radius, so we can determinethe distance around the circle. We start with the equation for the circumference of a circle
Therefore, the distance the man covers in one revolution is .
We know that speed is distance covered per unit time. So if we divide the distance covered by the time it took we will know how much distance was covered for every unit of time. No direction is used here because speed is a scalar.
Consider the point A in the diagram.
We know which way the man is running around the track and we know hisspeed. His velocity at point A will be his speed (the magnitude of the
velocity) plus his direction of motion (the direction of hisvelocity).
The instant that he arrives at A he is moving as indicated in thediagram.
His velocity will be
West.


Consider the point B in the diagram.
We know which way the man is running around the track and we know hisspeed. His velocity at point B will be his speed (the magnitude of the
velocity) plus his direction of motion (the direction of hisvelocity). The instant that he arrives at B he is moving as indicated in
the diagram.His velocity will be
South.


To determine the average velocity between A and B, we need the change in displacement between A and B and the change in time between A and B. Thedisplacement from A and B can be calculated by using the Theorem of Pythagoras:

Triangle AOB is isosceles and therefore angle BAO = 45 .
The direction is between west and south and is therefore southwest.
The final answer is: , southwest.
Because he runs at a constant rate, we know that his speed anywhere around the track will be the same. His average speed is .
To calculate average velocity we need his total displacement and his total time. His displacement is zero because he ends up where he started. Histime is . Using these we can calculate his average velocity:

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 10 physical science' conversation and receive update notifications?