7.5 Filtering: test sequences

When we design a filter, we design it for a purpose. For example, a moving average filter is often designed to pass relatively constant data whileaveraging out relatively variable data. In an effort to clarify the behavior of a filter, we typically analyze its response to a standard set of test signals. Wewill call the impulse , the step , and the complex exponential the standard test signals.

Unit Pulse Sequence. The unit pulse sequence is the sequence

This sequence, illustrated in Figure 1 , consists of all zeros except for a single one at $n=0$ . If the unit pulse sequence is passed through a moving average filter (whether finite or not), then the output is called the unit pulse response :

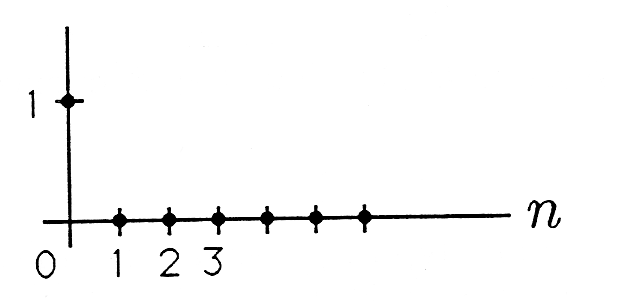
(Note that ${\delta }_{n-k}=0$ unless $n=k.$ ) So the unit pulse sequence may be used to read out the weights of a moving average filter. It is common practice to use $w_k$ (the $k^{th}$ weight) and $h_k$ (the $k^{th}$ impulse response) interchangeably.

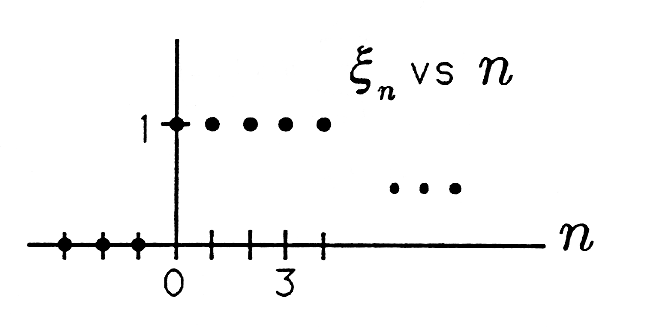
Unit Step Sequence. The unit step sequence is the sequence

This sequence is illustrated in Figure 2 . When this sequence is applied to a moving average filter, the result is the unit step response

The unit step response is just the sequence of partial sums of the unit pulse response.

Complex Exponential Sequence. The complex exponential sequence is the sequence

This sequence, illustrated in Figure 3 , is a “discrete-time phasor” that “ratchets” counterclockwise (CCW) as $k$ moves to $k+1$ and clockwise (CW) as $k$ moves to $k-1$ . Each time the phasor ratchets, it turns out an angle of $\theta$ . Why should such a sequence be a useful test sequence? There are two reasons.

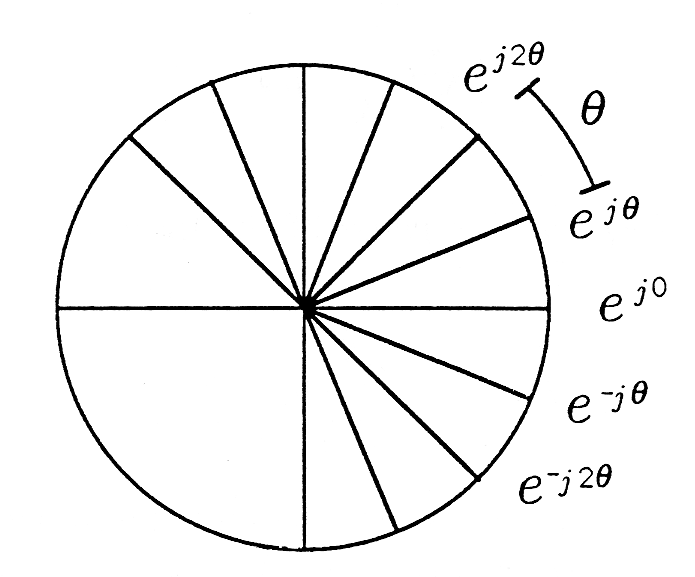
(i) $e^{jk\theta }$ represents (or codes) $cosk\theta$ . The real part of the sequence $e^{jk\theta }$ is the cosinusoidal sequence $cosk\theta$ :

Therefore the discrete-time phasor $e^{jk\theta }$ represents (or codes) $cosk\theta$ in the same way that the continuous-time phasor $e^{j\omega t}$ codes $cos\omega t$ . If the moving average filter

has real coefficients, we can get the response to a cosinusoidal sequence by taking the real part of the following sum:

In this formula, the sum

is called the complex frequency response of the filter and is given the symbol

This complex frequency response is just a complex number, with a magnitude $\left|H\right(e^{j\theta }\left)\right|$ and a phase arg $H\left(e^{j\theta }\right)$ . Therefore the output of the moving average filter is

This remarkable result says that the output is also cosinusoidal, but its amplitude is $\left|H\right(e^{j\theta }\left)\right|$ rather than 1, and its phase is $argH\left(e^{j\theta }\right)$ rather than 0. In the examples to follow, we will show that the complex “gain” $H\left(e^{j\theta }\right)$ can be highly selective in $\theta$ , meaning that cosines of some angular frequencies are passed with little attenuation while cosines of other frequencies are dramatically attenuated. By choosing the filter coefficients, we can design the frequency selectivity we would like to have.

(ii) ${\mathit{\text{e}}}^{jk\theta }$ is a sampled data version of $e^{j\omega t}$ . The discrete-time phasor $e^{jk\theta }$ can be produced physically by sampling the continuous-time phasor $e^{j\omega t}$ at the periodic sampling instants $t_k=kT$ :

The dimensions of $\theta$ are radians, the dimensions of $\omega$ are radians/second, and the dimensions of $T$ are seconds. We call $T$ the sampling interval and $\frac{1}{T}$ the sampling rate or sampling frequency. If the original angular frequency of thephasor $e^{j\omega t}$ is increased to $\omega +m\left(\frac{2\pi }{T}\right)$ , then the discrete-time phasor remains $e^{jk\theta }$ :

This means that all continuous-time phasors of the form $e^{j[\omega +m(2\pi /T\left)\right]t}$ “hide under the same alias” when viewed through the sampling operation. Thatis, the sampled-data phasor cannot distinguish the frequency $\omega$ from the frequency $\omega +m\frac{2\pi }{T}$ . In your subsequent courses you will study aliasing in more detail and study the Nyquist rule for sampling:

This rule says that you must sample signals at a rate $\left(\frac{1}{T}\right)$ that exceeds the bandwidth $\frac{\Omega }{2\pi }$ of the signal.

Let's pass the cosinusoidal sequence $u_k=$ cos $k\theta$ through the finite moving average filter

We know from our previous result that the output is

The complex frequency response for this example is

(Do you see your old friend, the finite sum formula, at work?) Let's try to manipulate the result into a more elegant form:

The magnitude of the function $H\left(e^{j\theta }\right)$ is

At $\theta =0$ , corresponding to a “DC phasor,” $H\left(e^{j\theta }\right)$ equals 1; at $\theta =\frac{2\pi }{N}$ $\left|H\right(e^{j\theta })=0|$ . The magnitude of the complex frequency response is plotted in Figure 4 .

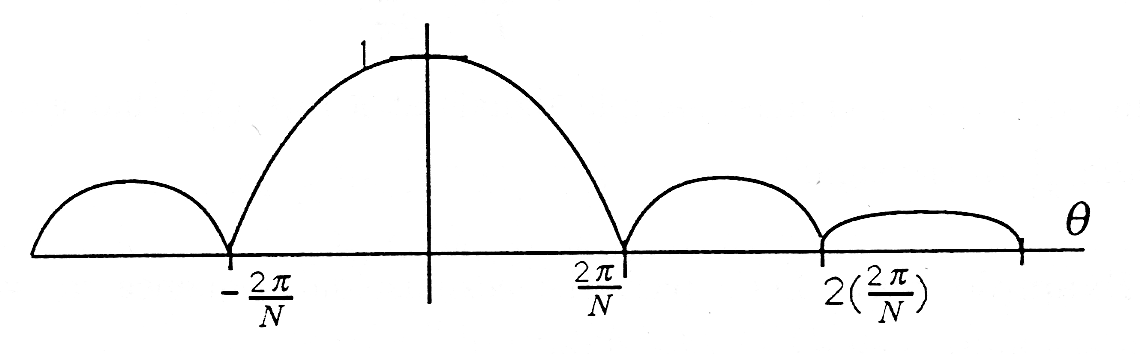
This result shows that the moving average filter is frequency selective, passing low frequencies with gain near 1 and high frequencies with gain near 0.