| << Chapter < Page | Chapter >> Page > |
Squaring both sides and simplifying yields
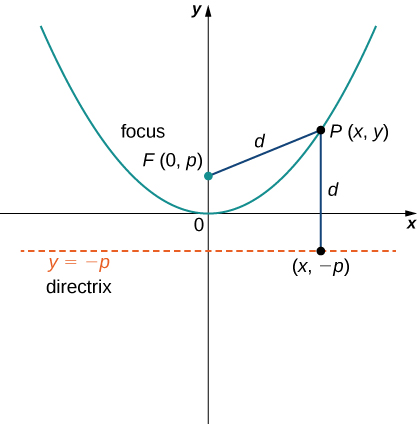
Now suppose we want to relocate the vertex. We use the variables to denote the coordinates of the vertex. Then if the focus is directly above the vertex, it has coordinates and the directrix has the equation Going through the same derivation yields the formula Solving this equation for y leads to the following theorem.
Given a parabola opening upward with vertex located at and focus located at where p is a constant, the equation for the parabola is given by
This is the standard form of a parabola.
We can also study the cases when the parabola opens down or to the left or the right. The equation for each of these cases can also be written in standard form as shown in the following graphs.
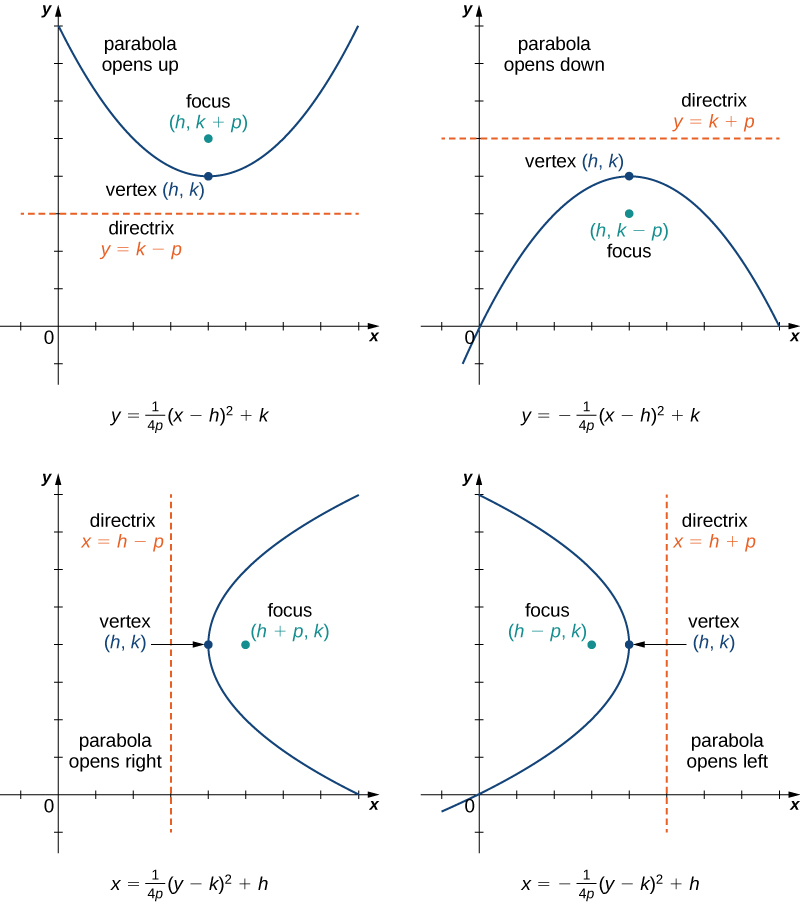
In addition, the equation of a parabola can be written in the general form , though in this form the values of h , k , and p are not immediately recognizable. The general form of a parabola is written as
The first equation represents a parabola that opens either up or down. The second equation represents a parabola that opens either to the left or to the right. To put the equation into standard form, use the method of completing the square.
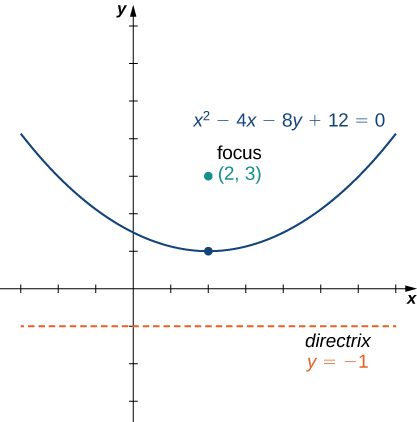
Put the equation into standard form and graph the resulting parabola.
Since y is not squared in this equation, we know that the parabola opens either upward or downward. Therefore we need to solve this equation for y, which will put the equation into standard form. To do that, first add to both sides of the equation:
The next step is to complete the square on the right-hand side. Start by grouping the first two terms on the right-hand side using parentheses:
Next determine the constant that, when added inside the parentheses, makes the quantity inside the parentheses a perfect square trinomial. To do this, take half the coefficient of x and square it. This gives Add 4 inside the parentheses and subtract 4 outside the parentheses, so the value of the equation is not changed:
Now combine like terms and factor the quantity inside the parentheses:
Finally, divide by 8:
This equation is now in standard form. Comparing this to [link] gives and The parabola opens up, with vertex at focus at and directrix The graph of this parabola appears as follows.
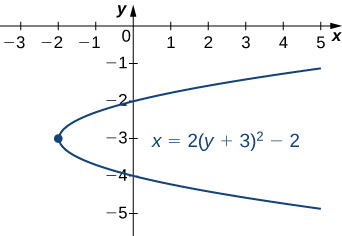
Put the equation into standard form and graph the resulting parabola.
The axis of symmetry of a vertical (opening up or down) parabola is a vertical line passing through the vertex. The parabola has an interesting reflective property. Suppose we have a satellite dish with a parabolic cross section. If a beam of electromagnetic waves, such as light or radio waves, comes into the dish in a straight line from a satellite (parallel to the axis of symmetry), then the waves reflect off the dish and collect at the focus of the parabola as shown.

Notification Switch
Would you like to follow the 'Calculus volume 2' conversation and receive update notifications?