| << Chapter < Page | Chapter >> Page > |
Probabilities are calculated by using technology. There are instructions in the chapter for the TI-83+ and TI-84 calculators.
If the area to the left is 0.0228, then the area to the right is .
The final exam scores in a statistics class were normally distributed with a mean of 63 and a standard deviation of 5.
Find the probability that a randomly selected student scored more than 65 on the exam.
Let a score on the final exam. ~ , where and
Draw a graph.
Then, find .
(calculator or computer)

The probability that one student scores more than 65 is 0.3446.
Using the TI-83+ or the TI-84 calculators, the calculation is as follows. Go into
2nd DISTR .
After pressing
2nd DISTR , press
2:normalcdf .
The syntax for the instructions are shown below.
normalcdf(lower value, upper value, mean, standard deviation)
For this problem:normalcdf(65,1E99,63,5) = 0.3446.
You get 1E99 ( =
) by pressing
1 , the
EE key (a 2nd key) and
then
99 . Or, you can enter
10^99 instead. The number
is way
out in the right tail of the normal curve. We are calculating the areabetween 65 and
. In some instances, the lower number of the area
might be -1E99 ( =
). The number
is way out in the left tail
of the normal curve.
. Area to the left is 0.6554.
Find the probability that a randomly selected student scored less than 85.
Draw a graph.
Then find . Shade the graph. (calculator or computer)
The probability that one student scores less than 85 is approximately 1 (or 100%).
The TI-instructions and answer are as follows:
normalcdf(0,85,63,5) = 1 (rounds to 1)
Find the 90th percentile (that is, find the score k that has 90 % of the scores below k and 10% of the scores above k).
Find the 90th percentile. For each problem or part of a problem, draw a new graph. Draw the x-axis. Shade the area that corresponds to the 90th percentile.
Let = the 90th percentile. is located on the x-axis. is the area to the left of . The 90th percentile separates the exam scores into those that are the same or lower than and those that are the same or higher. Ninety percent of the test scores are the same or lower than and 10% are the same or higher. is often called a critical value .
(calculator or computer)
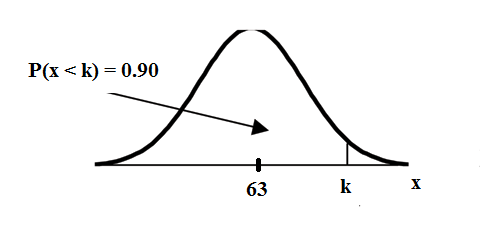
The 90th percentile is 69.4. This means that 90% of the test scores fall at
or below 69.4 and 10% fall at or above.For the TI-83+ or TI-84 calculators, use
invNorm in
2nd DISTR .
invNorm(area to the left, mean, standard deviation)For this problem,
invNorm(0.90,63,5) = 69.4
Find the 70th percentile (that is, find the score k such that 70% of scores are below k and 30% of the scores are above k).
Find the 70th percentile.
Draw a new graph and label it appropriately.
The 70th percentile is 65.6. This means that 70% of the test scores fall at or below 65.5 and 30% fall at or above.
invNorm(0.70,63,5) = 65.6
A computer is used for office work at home, research, communication, personal finances, education, entertainment, social networking and a myriad of other things. Suppose that the average number of hours a householdpersonal computer is used for entertainment is 2 hours per day. Assume the times for entertainment are normally distributed and the standard deviation for the times is half an hour.
Find the probability that a household personal computer is used between 1.8 and 2.75 hours per day.
Let = the amount of time (in hours) a household personal computer is used for entertainment. ~ where and .
Find .
The probability for which you are looking is the area between and
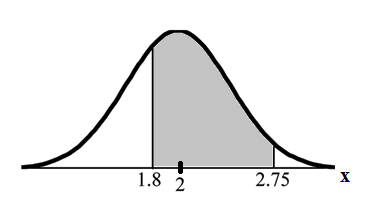
normalcdf(1.8,2.75,2,0.5) = 0.5886
The probability that a household personal computer is used between 1.8 and 2.75 hours per day for entertainment is 0.5886.
Find the maximum number of hours per day that the bottom quartile of households use a personal computer for entertainment.
To find the maximum number of hours per day that the bottom quartile of households uses a personal computer for entertainment, find the 25th percentile, , where .
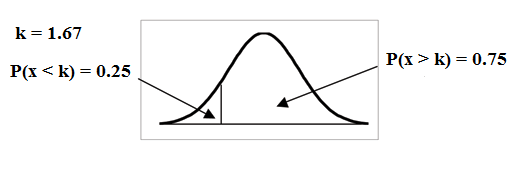
invNorm(0.25,2,.5) = 1.66
The maximum number of hours per day that the bottom quartile of households uses a personal computer for entertainment is 1.66 hours.

Notification Switch
Would you like to follow the 'Elementary statistics' conversation and receive update notifications?