7.2 Calculus of parametric curves  (Page 4/6)

We can summarize this method in the following theorem.

At this point a side derivation leads to a previous formula for arc length. In particular, suppose the parameter can be eliminated, leading to a function $y=F\left(x\right).$ Then $y\left(t\right)=F\left(x\left(t\right)\right)$ and the Chain Rule gives $y^{\prime }\left(t\right)=F^{\prime }\left(x\left(t\right)\right)x^{\prime }\left(t\right).$ Substituting this into [link] gives

Here we have assumed that $x^{\prime }\left(t\right)>0,$ which is a reasonable assumption. The Chain Rule gives $dx=x^{\prime }\left(t\right)dt,$ and letting $a=x\left(t_1\right)$ and $b=x\left(t_2\right)$ we obtain the formula

which is the formula for arc length obtained in the Introduction to the Applications of Integration .

Finding the arc length of a parametric curve

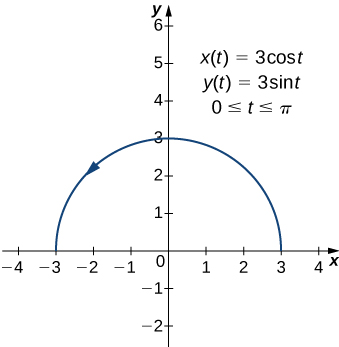
Find the arc length of the semicircle defined by the equations

$x\left(t\right)=3\text{cos}t,y\left(t\right)=3\text{sin}t,0\le t\le \pi .$

The values $t=0$ to $t=\pi$ trace out the red curve in [link] . To determine its length, use [link] :

$\begin{array}{cc}\hfill s& ={\displaystyle {\int }_{t_1}^{t_2}\sqrt{{\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2}dt}\hfill \\ & ={\displaystyle {\int }_0^{\pi }\sqrt{{\left(\mathrm{-3}\text{sin}t\right)}^2+{\left(3\text{cos}t\right)}^2}dt}\hfill \\ & ={\displaystyle {\int }_0^{\pi }\sqrt{9{\text{sin}}^{2}t+9{\text{cos}}^{2}t}dt}\hfill \\ & ={\displaystyle {\int }_0^{\pi }\sqrt{9\left({\text{sin}}^{2}t+{\text{cos}}^{2}t\right)}dt}\hfill \\ & ={\displaystyle {\int }_0^{\pi }3dt}={3t|}_0^{\pi }=3\pi .\hfill \end{array}$

Note that the formula for the arc length of a semicircle is $\pi r$ and the radius of this circle is 3. This is a great example of using calculus to derive a known formula of a geometric quantity.

Got questions? Get instant answers now!

Got questions? Get instant answers now!

We now return to the problem posed at the beginning of the section about a baseball leaving a pitcher’s hand. Ignoring the effect of air resistance (unless it is a curve ball!), the ball travels a parabolic path. Assuming the pitcher’s hand is at the origin and the ball travels left to right in the direction of the positive x -axis, the parametric equations for this curve can be written as

where t represents time. We first calculate the distance the ball travels as a function of time. This distance is represented by the arc length. We can modify the arc length formula slightly. First rewrite the functions $x\left(t\right)$ and $y\left(t\right)$ using v as an independent variable, so as to eliminate any confusion with the parameter t :

Then we write the arc length formula as follows:

The variable v acts as a dummy variable that disappears after integration, leaving the arc length as a function of time t. To integrate this expression we can use a formula from Appendix A ,

We set $a=140$ and $u=\mathrm{-32}v+2.$ This gives $du=\mathrm{-32}dv,$ so $dv=-\frac{1}{32}du.$ Therefore

and

This function represents the distance traveled by the ball as a function of time. To calculate the speed, take the derivative of this function with respect to t. While this may seem like a daunting task, it is possible to obtain the answer directly from the Fundamental Theorem of Calculus: