| << Chapter < Page | Chapter >> Page > |
Suppose we have two collections of objects that we combine together to form a third collection. For example,

We are combining a collection of four objects with a collection of three objects to obtain a collection of seven objects.
In addition, the numbers being added are called addends or terms , and the total is called the sum . The plus symbol (+) is used to indicate addition, and the equal symbol (=) is used to represent the word "equal." For example, means "four added to three equals seven."
Addition is easily visualized on the number line. Let's visualize the addition of 4 and 3 using the number line.
To find ,
Thus, .

We'll study the process of addition by considering the sum of 25 and 43.
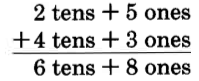
We write this as 68.
We can suggest the following procedure for adding whole numbers using this example.
To add whole numbers ,
The process:
Add 276 and 103.
Add 1459 and 130
In each of these examples, each individual sum does not exceed 9. We will examine individual sums that exceed 9 in the next section.
Perform each addition. Show the expanded form in problems 1 and 2.
Add 63 and 25.
88
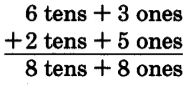
Add 4,026 and 1,501.
5,527

Add 231,045 and 36,121.
267,166
It often happens in addition that the sum of the digits in a column will exceed 9. This happens when we add 18 and 34. We show this in expanded form as follows.
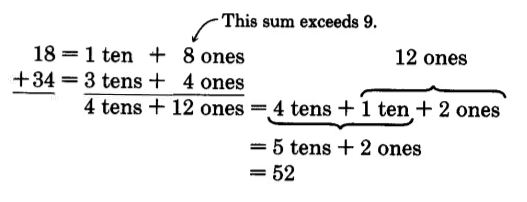
Notice that when we add the 8 ones to the 4 ones we get 12 ones. We then convert the 12 ones to 1 ten and 2 ones. In vertical addition, we show this conversion by carrying the ten to the tens column. We write a 1 at the top of the tens column to indicate the carry. This same example is shown in a shorter form as follows:
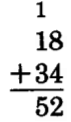 Write 2, carry 1 ten to the top of the next column to the left.
Write 2, carry 1 ten to the top of the next column to the left.
Perform the following additions. Use the process of carrying when needed.

Notification Switch
Would you like to follow the 'Contemporary math applications' conversation and receive update notifications?