| << Chapter < Page | Chapter >> Page > |
Solve the following initial-value problem and graph the solution:
The following initial-value problem models the position of an object with mass attached to a spring. Spring-mass systems are examined in detail in Applications . The solution to the differential equation gives the position of the mass with respect to a neutral (equilibrium) position (in meters) at any given time. (Note that for spring-mass systems of this type, it is customary to define the downward direction as positive.)
Solve the initial-value problem and graph the solution. What is the position of the mass at time sec? How fast is the mass moving at time sec? In what direction?
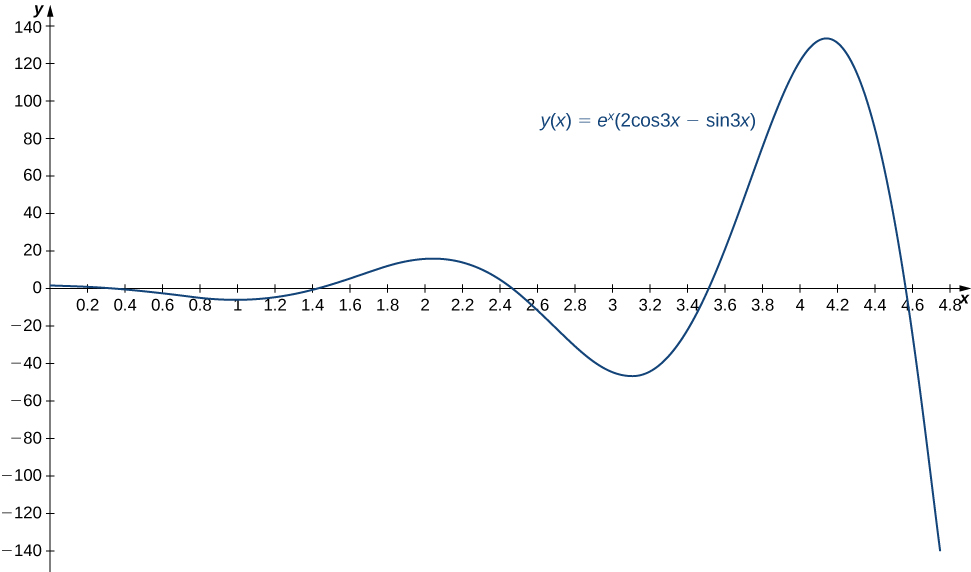
In [link] c. we found the general solution to this differential equation to be
Then
When we have and Applying the initial conditions, we obtain
Thus, and the solution to the initial value problem is
This solution is represented in the following graph. At time the mass is at position m below equilibrium.
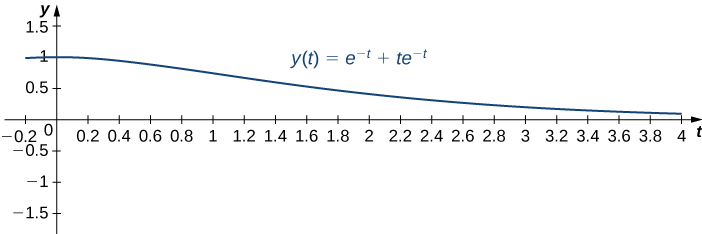
To calculate the velocity at time we need to find the derivative. We have so
Then At time the mass is moving upward at 0.3679 m/sec.
Suppose the following initial-value problem models the position (in feet) of a mass in a spring-mass system at any given time. Solve the initial-value problem and graph the solution. What is the position of the mass at time sec? How fast is it moving at time sec? In what direction?
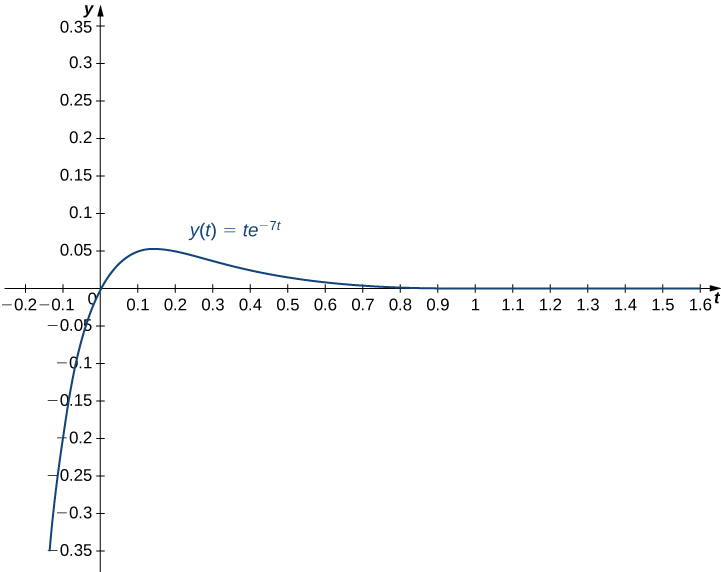
At time
The mass is 0.0367 ft below equilibrium. At time
The mass is moving downward at a speed of 0.1490 ft/sec.
In [link] f. we solved the differential equation and found the general solution to be If possible, solve the boundary-value problem if the boundary conditions are the following:
We have
Classify each of the following equations as linear or nonlinear. If the equation is linear, determine whether it is homogeneous or nonhomogeneous.
For each of the following problems, verify that the given function is a solution to the differential equation. Use a graphing utility to graph the particular solutions for several values of c 1 and c 2 . What do the solutions have in common?
[T]
Find the general solution to the linear differential equation.
Solve the initial-value problem.
Solve the boundary-value problem, if possible.
Find a differential equation with a general solution that is
Find a differential equation with a general solution that is
For each of the following differential equations:
(Principle of superposition) Prove that if and are solutions to a linear homogeneous differential equation, then the function where and are constants, is also a solution.
Prove that if a, b, and c are positive constants, then all solutions to the second-order linear differential equation approach zero as ( Hint: Consider three cases: two distinct roots, repeated real roots, and complex conjugate roots.)

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?