| << Chapter < Page | Chapter >> Page > |
The simplest numerical filter is the simple averaging filter. This filter is defined by the equation
The filter output x is the average of the N filter inputs , u N . These inputs may be real or complex numbers, and x may be real or complex. This simple averaging filter is illustrated in Figure 1 .
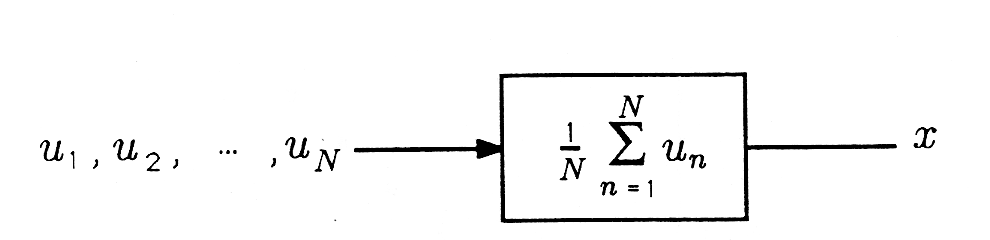
If the averaging filter is excited by the constant sequence , then the output is
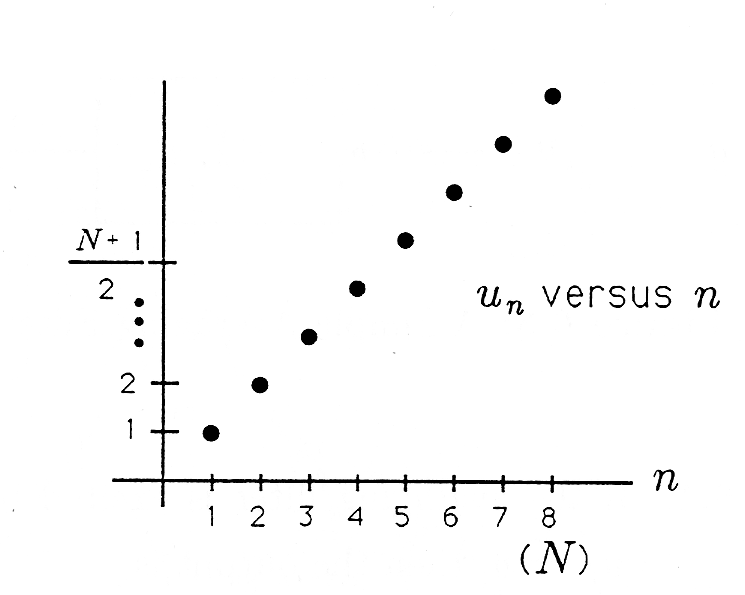
The output is, truly, the average of the inputs. Now suppose the filter is excited by the linearly increasing sequence
This sequence is plotted in Figure 2 . How do we sum such a sequence in order to produce the average ? For even, the average may be written as
Each pair-sum in parentheses equals , and there are such pair-sums, so the average is
This is certainly a reasonable answer for the average of a linearly increasing sequence. See Figure 2 .
General Sum Formula. Suppose the input to the simple averaging filter is the polynomial sequence
where is a non-negative integer such as . The output of the filter is
We rewrite as to remind ourselves that we are averaging numbers, each of which is . For example, when and ,
Rather than study the average , we will study the sum and divide by at the very end:
The sum may be rewritten as the sum
This result is very important because it tells us that the sum , viewed as a function of , obeys a recursion in which is just the sum using one less input, namely, , plus . Now, since polynomials are the most general functions that obey such recursions, we know that must be a polynomial of order in the variable :
Let's check to see that this polynomial really can obey the required recursion. First note that is the following polynomial:
The term produces . (Remember the binomial expansion?) Therefore the difference between and is
This recursion is general enough to produce the difference N k provided we can solve for , to make and . We know that for , so we know that , meaning that the polynomial for can really be written as
In order to solve for the coefficients of this polynomial, we propose to write out our equationfor as follows:
Using the linear algebra we learned earlier, we may write these equations as the matrix equation
The terms on the right-hand side of the equal sign are “initial conditions” that tell us how the sum begins for . These initial conditions must be computed directly. (For example, ) Then the linear system of equations in unknowns may be solved for . The solution for is then complete, and we may use it to solve for for arbitrary .
When , we have the following equation for the coefficients , and in the polynomial :
Exponential Sums. When the input to an averaging filter is the sequence
we say that the input is exponential (or geometric). Typical sequences are illustrated in Figure 6.5 for , and . Don't let it throw you that we have changed the index to run from 0 to rather than from 1 to . This change is not fundamentally important, but it simplifies our study. The sum of the inputs is

How do we evaluate this sum? Well, we note that the sum is
Therefore, provided , the sum is
This formula, discovered already in the chapter covering the functions and , works for . When , then :
When , then for , and we have the asymptotic formula
Recursive Computation. Every sum of the form
obeys the recursion
This means that when summing numbers you may “use them and discard them.” That is, you do not need to read them, store them, and sum them.
You may read to form and discard ; add to and discard ; add to ; and continue.

This is very important for hardware and software implementations of running sums. You need only store the current sum, not the measurements that produced it. Two illustrations of the recursion are provided in Figure 4 . The diagram on the left is self-explanatory. The diagram on the right says that the sum is stored in a memory location, to be added to to produce , which is then stored back in the memory location to be added to , and so on.

Notification Switch
Would you like to follow the 'A first course in electrical and computer engineering' conversation and receive update notifications?