| << Chapter < Page | Chapter >> Page > |
Recall that the flux form of Green’s theorem states that Therefore, the divergence theorem is a version of Green’s theorem in one higher dimension.
The proof of the divergence theorem is beyond the scope of this text. However, we look at an informal proof that gives a general feel for why the theorem is true, but does not prove the theorem with full rigor. This explanation follows the informal explanation given for why Stokes’ theorem is true.
Let B be a small box with sides parallel to the coordinate planes inside E ( [link] ). Let the center of B have coordinates and suppose the edge lengths are and ( [link] (b)). The normal vector out of the top of the box is k and the normal vector out of the bottom of the box is The dot product of with k is R and the dot product with is The area of the top of the box (and the bottom of the box) is
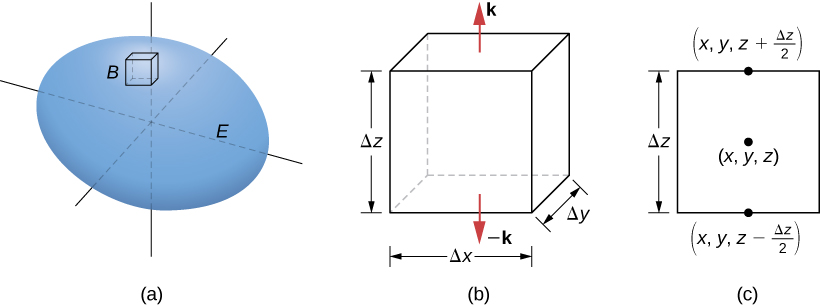
The flux out of the top of the box can be approximated by ( [link] (c)) and the flux out of the bottom of the box is If we denote the difference between these values as then the net flux in the vertical direction can be approximated by However,
Therefore, the net flux in the vertical direction can be approximated by Similarly, the net flux in the x -direction can be approximated by and the net flux in the y -direction can be approximated by Adding the fluxes in all three directions gives an approximation of the total flux out of the box:
This approximation becomes arbitrarily close to the value of the total flux as the volume of the box shrinks to zero.
The sum of over all the small boxes approximating E is approximately On the other hand, the sum of over all the small boxes approximating E is the sum of the fluxes over all these boxes. Just as in the informal proof of Stokes’ theorem, adding these fluxes over all the boxes results in the cancelation of a lot of the terms. If an approximating box shares a face with another approximating box, then the flux over one face is the negative of the flux over the shared face of the adjacent box. These two integrals cancel out. When adding up all the fluxes, the only flux integrals that survive are the integrals over the faces approximating the boundary of E . As the volumes of the approximating boxes shrink to zero, this approximation becomes arbitrarily close to the flux over S .
□
Verify the divergence theorem for vector field and surface S that consists of cone and the circular top of the cone (see the following figure). Assume this surface is positively oriented.
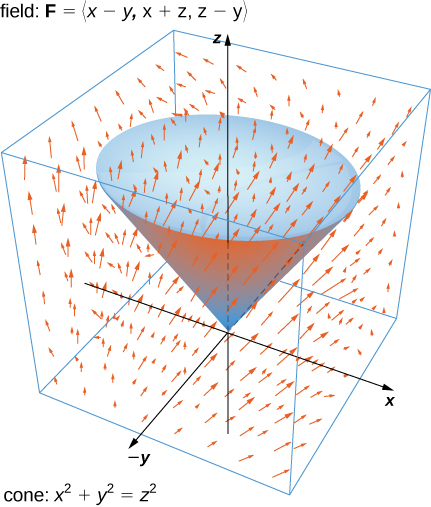
Let E be the solid cone enclosed by S . To verify the theorem for this example, we show that by calculating each integral separately.
To compute the triple integral, note that and therefore the triple integral is
The volume of a right circular cone is given by In this case, Therefore,
To compute the flux integral, first note that S is piecewise smooth; S can be written as a union of smooth surfaces. Therefore, we break the flux integral into two pieces: one flux integral across the circular top of the cone and one flux integral across the remaining portion of the cone. Call the circular top and the portion under the top We start by calculating the flux across the circular top of the cone. Notice that has parameterization
Then, the tangent vectors are and Therefore, the flux across is
We now calculate the flux over A parameterization of this surface is
The tangent vectors are and so the cross product is
Notice that the negative signs on the x and y components induce the negative (or inward) orientation of the cone. Since the surface is positively oriented, we use vector in the flux integral. The flux across is then
The total flux across S is
and we have verified the divergence theorem for this example.

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?