| << Chapter < Page | Chapter >> Page > |
Because charges ordinarily cannot escape a conductor, the magnetic force on charges moving in a conductor is transmitted to the conductor itself.
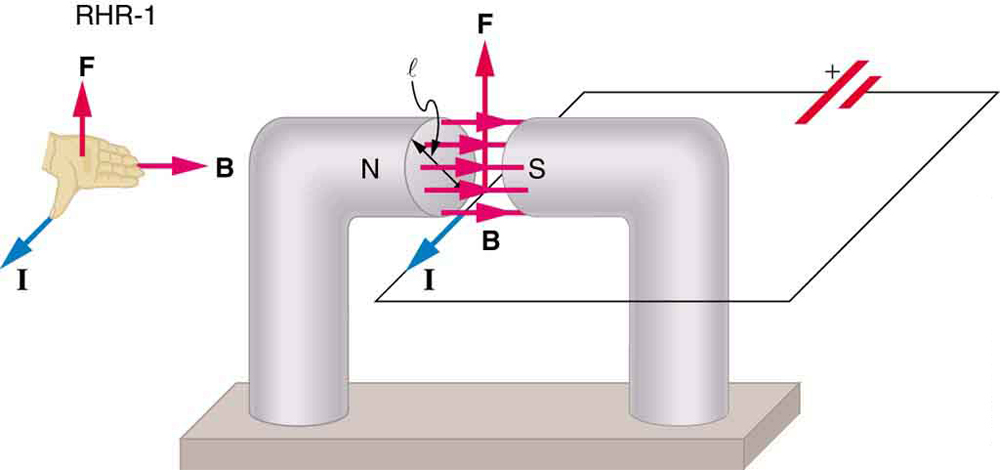
We can derive an expression for the magnetic force on a current by taking a sum of the magnetic forces on individual charges. (The forces add because they are in the same direction.) The force on an individual charge moving at the drift velocity is given by . Taking to be uniform over a length of wire and zero elsewhere, the total magnetic force on the wire is then , where is the number of charge carriers in the section of wire of length . Now, , where is the number of charge carriers per unit volume and is the volume of wire in the field. Noting that , where is the cross-sectional area of the wire, then the force on the wire is . Gathering terms,
Because (see Current ),
is the equation for magnetic force on a length of wire carrying a current in a uniform magnetic field , as shown in [link] . If we divide both sides of this expression by , we find that the magnetic force per unit length of wire in a uniform field is . The direction of this force is given by RHR-1, with the thumb in the direction of the current . Then, with the fingers in the direction of , a perpendicular to the palm points in the direction of , as in [link] .
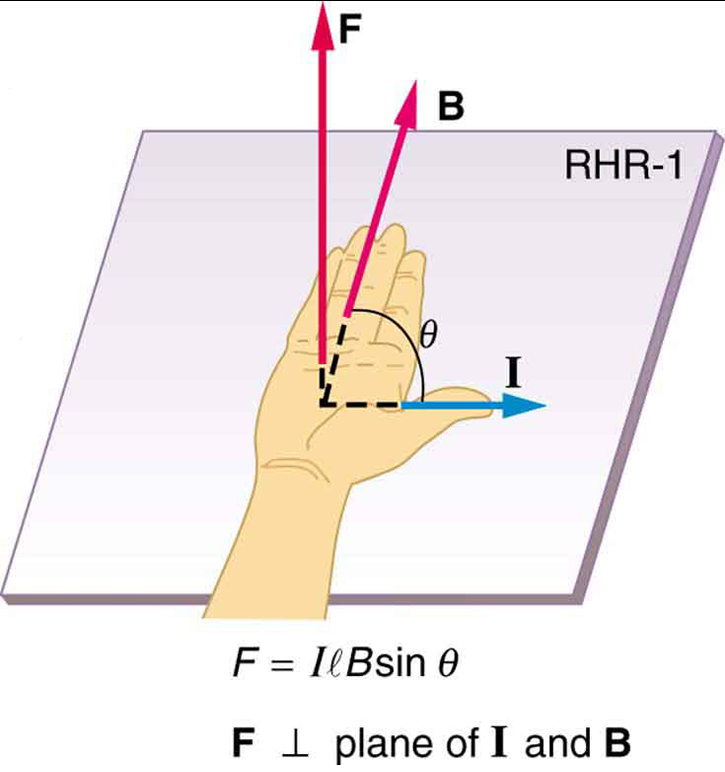
Calculate the force on the wire shown in [link] , given , , and .
Strategy
The force can be found with the given information by using and noting that the angle between and is , so that .
Solution
Entering the given values into yields
The units for tesla are ; thus,
Discussion
This large magnetic field creates a significant force on a small length of wire.
Magnetic force on current-carrying conductors is used to convert electric energy to work. (Motors are a prime example—they employ loops of wire and are considered in the next section.) Magnetohydrodynamics (MHD) is the technical name given to a clever application where magnetic force pumps fluids without moving mechanical parts. (See [link] .)
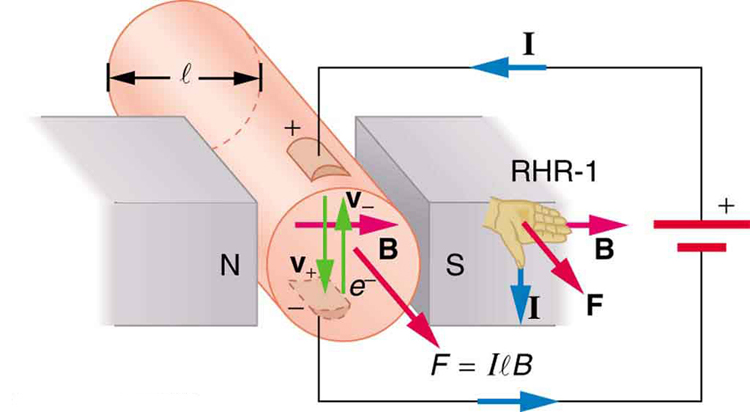
A strong magnetic field is applied across a tube and a current is passed through the fluid at right angles to the field, resulting in a force on the fluid parallel to the tube axis as shown. The absence of moving parts makes this attractive for moving a hot, chemically active substance, such as the liquid sodium employed in some nuclear reactors. Experimental artificial hearts are testing with this technique for pumping blood, perhaps circumventing the adverse effects of mechanical pumps. (Cell membranes, however, are affected by the large fields needed in MHD, delaying its practical application in humans.) MHD propulsion for nuclear submarines has been proposed, because it could be considerably quieter than conventional propeller drives. The deterrent value of nuclear submarines is based on their ability to hide and survive a first or second nuclear strike. As we slowly disassemble our nuclear weapons arsenals, the submarine branch will be the last to be decommissioned because of this ability (See [link] .) Existing MHD drives are heavy and inefficient—much development work is needed.

Notification Switch
Would you like to follow the 'General physics ii phy2202ca' conversation and receive update notifications?