6.6 Surface integrals (Page 5/27)

Calculus volume 3 Page 5 / 27

Δ S_{i j} \approx ‖ (Δ u t_{u} (P_{i j})) \times (Δ v t_{v} (P_{i j})) ‖ = ‖ t_{u} (P_{i j}) \times t_{v} (P_{i j}) ‖ Δ u Δ v .

Varying point $P_{i j}$ over all pieces $S_{i j}$ and the previous approximation leads to the following definition of surface area of a parametric surface ( [link] ).

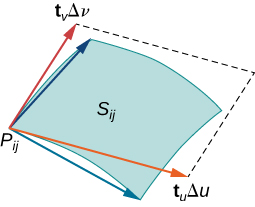
A surface S_ij that looks like a curved parallelogram. Point P_ij is at the bottom left corner, and two blue arrows stretch from this point to the upper left and lower right corners of the surface. Two red arrows also stretch out from this point, and they are labeled t_v delta v and t_u delta u. These form two sides of a parallelogram that approximates the piece of surface of S_ij. The other two sides are drawn as dotted lines. — The parallelogram spanned by $t_{u}$ and $t_{v}$ approximates the piece of surface $S_{i j} .$

Definition

Let $r (u, v) = ⟨ x (u, v), y (u, v), z (u, v) ⟩$ with parameter domain D be a smooth parameterization of surface S . Furthermore, assume that S is traced out only once as $(u, v)$ varies over D . The surface area of S is

\iint_{D} ‖ t_{u} \times t_{v} ‖ d A,

where $t_{u} = ⟨ \frac{\partial x}{\partial u}, \frac{\partial y}{\partial u}, \frac{\partial z}{\partial u} ⟩$ and $t_{v} = ⟨ \frac{\partial x}{\partial v}, \frac{\partial y}{\partial v}, \frac{\partial z}{\partial v} ⟩ .$

Calculating surface area

Calculate the lateral surface area (the area of the “side,” not including the base) of the right circular cone with height h and radius r .

Before calculating the surface area of this cone using [link] , we need a parameterization. We assume this cone is in $ℝ^{3}$ with its vertex at the origin ( [link] ). To obtain a parameterization, let $α$ be the angle that is swept out by starting at the positive z -axis and ending at the cone, and let $k = tan α .$ For a height value v with $0 \leq v \leq h,$ the radius of the circle formed by intersecting the cone with plane $z = v$ is $k v .$ Therefore, a parameterization of this cone is

s (u, v) = ⟨ k v cos u, k v sin u, v ⟩, 0 \leq u < 2 π, 0 \leq v \leq h .

The idea behind this parameterization is that for a fixed v value, the circle swept out by letting u vary is the circle at height v and radius kv . As v increases, the parameterization sweeps out a “stack” of circles, resulting in the desired cone.

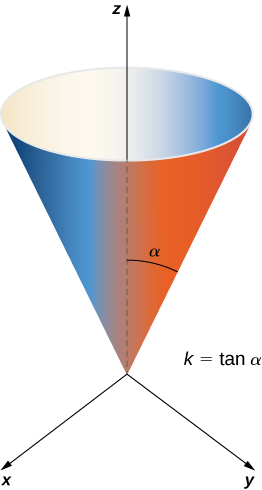
A right circular cone in three dimensions, opening upwards on the z axis. It has radius r = kh and height h with the given parameterization. Alpha is the angle that is swept out by starting at the positive z-axis and ending at the cone. It is noted that k is equal to the tangent of alpha. — The right circular cone with radius *r = kh* and height h has parameterization $s (u, v) = ⟨ k v cos u, k v sin u, v ⟩, 0 \leq u < 2 π, 0 \leq v \leq h .$

With a parameterization in hand, we can calculate the surface area of the cone using [link] . The tangent vectors are $t_{u} = ⟨ − k v sin u, k v cos u, 0 ⟩$ and $t_{v} = ⟨ k cos u, k sin u, 1 ⟩ .$ Therefore,

\begin{matrix} t_{u} \times t_{v} & = | \begin{matrix} i & j & k \\ − k v sin u & k v cos u & 0 \\ k cos u & k sin u & 1 \end{matrix} | \\ = ⟨ k v cos u, k v sin u, − k^{2} v {sin}^{2} u - k^{2} v {cos}^{2} u ⟩ \\ = ⟨ k v cos u, k v sin u, − k^{2} v ⟩ . \end{matrix}

The magnitude of this vector is

\begin{matrix} ‖ ⟨ k v cos u, k v sin u, − k^{2} v ⟩ ‖ & = \sqrt{k^{2} v^{2} {cos}^{2} u + k^{2} v^{2} {sin}^{2} u + k^{4} v^{2}} \\ = \sqrt{k^{2} v^{2} + k^{4} v^{2}} \\ = k v \sqrt{1 + k^{2}} . \end{matrix}

By [link] , the surface area of the cone is

\begin{matrix} \iint_{D} ‖ t_{u} \times t_{v} ‖ d A & = \int_{0}^{h} \int_{0}^{2 π} k v \sqrt{1 + k^{2}} d u d v \\ = 2 π k \sqrt{1 + k^{2}} \int_{0}^{h} v d v \\ = 2 π k \sqrt{1 + k^{2}} {[\frac{v^{2}}{2}]}_{0}^{h} \\ = π k h^{2} \sqrt{1 + k^{2}} . \end{matrix}

Since $k = tan α = r / h,$

\begin{matrix} π k h^{2} \sqrt{1 + k^{2}} & = π \frac{r}{h} h^{2} \sqrt{1 + \frac{r^{2}}{h^{2}}} \\ = π r h \sqrt{1 + \frac{r^{2}}{h^{2}}} \\ = π r \sqrt{h^{2} + h^{2} (\frac{r^{2}}{h^{2}})} \\ = π r \sqrt{h^{2} + r^{2}} . \end{matrix}

Therefore, the lateral surface area of the cone is $π r \sqrt{h^{2} + r^{2}} .$

Got questions? Get instant answers now!

Find the surface area of the surface with parameterization $r (u, v) = ⟨ u + v, u^{2}, 2 v ⟩, 0 \leq u \leq 3, 0 \leq v \leq 2 .$

$\approx 43.02$

Got questions? Get instant answers now!

Calculating surface area

Show that the surface area of the sphere $x^{2} + y^{2} + z^{2} = r^{2}$ is $4 π r^{2} .$

The sphere has parameterization

⟨ r cos θ sin ϕ, r sin θ sin ϕ, r cos ϕ ⟩, 0 \leq θ < 2 π, 0 \leq ϕ \leq π .

The tangent vectors are

t_{θ} = ⟨ − r sin θ sin ϕ, r cos θ sin ϕ, 0 ⟩ and t_{ϕ} = ⟨ r cos θ cos ϕ, r sin θ cos ϕ, − r sin ϕ ⟩ .

Therefore,

\begin{matrix} t_{ϕ} \times t_{θ} & = ⟨ r^{2} cos θ {sin}^{2} ϕ, r^{2} sin θ {sin}^{2} ϕ, r^{2} {sin}^{2} θ sin ϕ cos ϕ + r^{2} {cos}^{2} θ sin ϕ cos ϕ ⟩ \\ = ⟨ r^{2} cos θ {sin}^{2} ϕ, r^{2} sin θ {sin}^{2} ϕ, r^{2} sin ϕ cos ϕ ⟩ . \end{matrix}

Now,

\begin{matrix} ‖ t_{ϕ} \times t_{θ} & = \sqrt{r^{4} {sin}^{4} ϕ {cos}^{2} θ + r^{4} {sin}^{4} ϕ {sin}^{2} θ + r^{4} {sin}^{2} ϕ {cos}^{2} ϕ} \\ = \sqrt{r^{4} {sin}^{4} ϕ + r^{4} {sin}^{2} ϕ {cos}^{2} ϕ} \\ = r^{2} \sqrt{{sin}^{2} ϕ} \\ = r sin ϕ . \end{matrix}

Notice that $sin ϕ \geq 0$ on the parameter domain because $0 \leq ϕ < π,$ and this justifies equation $\sqrt{{sin}^{2} ϕ} = sin ϕ .$ The surface area of the sphere is

\int_{0}^{2 π} \int_{0}^{π} r^{2} sin ϕ d ϕ d θ = r^{2} \int_{0}^{2 π} 2 d θ = 4 π r^{2} .

We have derived the familiar formula for the surface area of a sphere using surface integrals.

Got questions? Get instant answers now!

Show that the surface area of cylinder $x^{2} + y^{2} = r^{2}, 0 \leq z \leq h$ is $2 π r h .$ Notice that this cylinder does not include the top and bottom circles.

With the standard parameterization of a cylinder, [link] shows that the surface area is $2 π r h .$

Got questions? Get instant answers now!

<< Chapter < Page Page > Chapter >>

Practice Key Terms 12

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Calculus volume 3. OpenStax CNX. Feb 05, 2016 Download for free at http://legacy.cnx.org/content/col11966/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?

Ask

	2 Human A&P 2- Test 2 By Madison Christian Start Flashcards
	38 Biology 38 The Musculoskeletal System MCQ By OpenStax Start Quiz
©flickr: Dutch	Las Vegas Timeshare By Donyea Sweets Start Test
	1 Endocrine System MCQ By Nick Swain Start Quiz
©flickr:	Dairy Cattle Evaluation Exam By Katy Keilers Start Exam
	28 Biology 28 Invertebrates MCQ By OpenStax Start Quiz
	Business Statistics By David Bourgeois Start Quiz
©flickr:	Anatomy Physiology By Jemekia Weeden Start Quiz
	2 SCEA Java Architect By JavaChamp Team Start Exam
©flickr: Miguel	Protozoal and Parasitic Infections By Cath Yu Start Quiz