| << Chapter < Page | Chapter >> Page > |
For the following exercises, determine whether the statement is true or false .
If the coordinate functions of have continuous second partial derivatives, then equals zero.
All vector fields of the form are conservative.
If F is a constant vector field then
For the following exercises, find the curl of F .
For the following exercises, find the divergence of F .
For the following exercises, determine whether each of the given scalar functions is harmonic.
If and find
Find given that where
Find the divergence of F for vector field
For the following exercises, use and
Let where F is defined on Find
For the following exercises, use a computer algebra system to find the curl of the given vector fields.
For the following exercises, find the divergence of F at the given point.
at (1, 2, 1)
For the following exercises, find the curl of F at the given point.
at (3, 2, 0)
at (0, 0, 3)
Given vector field on domain is F conservative?
Given vector field on domain is F conservative?
F is conservative.
Find the work done by force field in moving an object from P (0, 1) to Q (2, 0). Is the force field conservative?
Compute curl
For the following exercises, consider a rigid body that is rotating about the x -axis counterclockwise with constant angular velocity If P is a point in the body located at the velocity at P is given by vector field
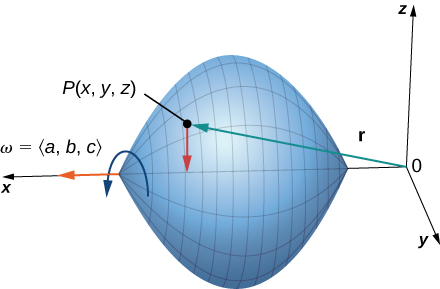
In the following exercises, suppose that and
Does necessarily have zero divergence?
Does necessarily have zero divergence?
does not have zero divergence.
In the following exercises, suppose a solid object in has a temperature distribution given by The heat flow vector field in the object is where is a property of the material. The heat flow vector points in the direction opposite to that of the gradient, which is the direction of greatest temperature decrease. The divergence of the heat flow vector is
Compute the heat flow vector field.
[T] Consider rotational velocity field If a paddlewheel is placed in plane with its axis normal to this plane, using a computer algebra system, calculate how fast the paddlewheel spins in revolutions per unit time.

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?