| << Chapter < Page | Chapter >> Page > |
This module relates circular convolution of periodic signals in the time domain to multiplication in the frequency domain.
Given a signal
with Fourier coefficients
and a signal
with Fourier coefficients
,
we can define a new signal,
,
where
We find that the
Fourier
Series representation of
,
,
is such that
.
is the
circular convolution of two periodic signals and is equivalent to the convolution
over one interval,
Take a look at a square pulse with a period of T.
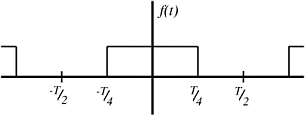
For this signal
Take a look at a triangle pulse train with a period of T.

This signal is created by circularly convolving the square pulse with itself. The Fourier coefficients for this signal are
Find the Fourier coefficients of the signal that is created when the square pulse and the triangle pulse are convolved.
Circular convolution in the time domain is equivalent to multiplication of the Fourier coefficients in the frequency domain.

Notification Switch
Would you like to follow the 'Signals and systems' conversation and receive update notifications?